高中物理匀速圆周运动试题

自行车的小齿轮A、大齿轮B、后轮C是相互关联的三个转动部分，且半径R_B＝4R_A、R_C＝8R_A，如图所示.当自行车正常骑行时A、B、C三轮边缘的向心加速度的大小之比a_A∶a_B∶a_C等于

A．1∶1∶8       B．4∶1∶4
C．4∶1∶32      D．1∶2∶4

如图所示，游乐场有一水上转台，可在水平面内匀速转动，沿半径方向面对面手拉手坐着甲、乙两个小孩，他们与盘间的动摩擦因数相同，当圆盘转速缓慢加快到两小孩刚好要发生滑动时，两小孩突然松手，则两小孩的运动情况是（   ）

A．两小孩均沿半径方向滑出后落入水中

B．两小孩仍随圆盘一起做匀速圆周运动，不会发生滑动而落入水中

C．甲仍随圆盘一起做匀速圆周运动，乙发生滑动最终落入水中

D．不知道甲乙质量关系，所以运动情况无法确定

2013年6月我国宇航员在天宫一号空间站中进行了我国首次太空授课活动，展示了许多在地面上无法实现的实验现象。假如要在空间站再次进行授课活动，下列我们曾在实验室中进行的实验，若移到空间站也能够实现操作的有

A．利用托盘天平测质量

B．利用弹簧测力计测拉力

C．利用自由落体验证机械能守恒定律

D．测定单摆做简谐运动的周期

如图所示，甲、乙两水平圆盘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲无打滑转动．甲圆盘与乙圆盘的半径之比为r_甲∶r_乙＝2∶1，两圆盘和小物体m₁、m₂之间的动摩擦因数相同，m₁距O点为2r，m₂距O′点为r，当甲缓慢转动起来且转速慢慢增加时（ ）．

A．与圆盘相对滑动前m1与m2的角速度之比ω1∶ω2＝2∶1

B．与圆盘相对滑动前m1与m2的向心加速度之比a1∶a2＝1∶2

C．随转速慢慢增加，m1先开始滑动

D．随转速慢慢增加，m2先开始滑动

如图所示为一皮带传动装置，右轮的半径为r，a是它边缘上的一点．左侧是一轮轴，大轮的半径为4r，小轮的半径为2r．b点在小轮上，到小轮中心的距离为r．c点和d点分别位于小轮和大轮的边缘上．若在传动过程中，皮带不打滑．则（　　）

A．a点与b点的线速度大小相等

B．a点与b点的角速度大小相等

C．a点与c点的线速度大小相等

D．a点与d点的向心加速度大小相等

某原子电离后其核外只有一个电子，若该电子在原子核的静电力作用下绕核做匀速圆周运动，那么电子运动的

A．半径越大，加速度越大	B．半径越小，周期越大
C．半径越大，角速度越小	D．半径越小，线速度越小

如图所示，甲、乙两水平圆盘紧靠在一起，大圆盘为主动轮，乙靠摩擦随甲无滑动地转动。大、小圆盘的半径之比为3∶1，两圆盘和小物体m₁、m₂间的动摩擦因数相同。m₁距甲盘圆心O点2r，m₂距乙盘圆心O′点r，当甲缓慢转动且转速慢慢增加时

A．物块相对盘开始滑动前，m1与m2的角速度之比为3∶1

B．物块相对盘开始滑动前，m1与m2的向心加速度之比为2∶9

C．随转速慢慢增加，m1先开始滑动

D．随转速慢慢增加，m2先开始滑动

“超级地球”是指围绕恒星公转的类地行星 科学家们发现有两颗未知质量的不同“超级地球”环绕同一颗恒星公转，周期分别为10天和20天 根据上述信息可以计算两颗“超级地球”（ ）
A 质量之比
B 所受的引力之比
C 角速度之比
D 向心加速度之比

"旋转纽扣"是一种传统游戏。如图，先将纽扣绕几圈，使穿过纽扣的两股细绳拧在一起，然后用力反复拉绳的两端，纽扣正转和反转会交替出现。拉动多次后，纽扣绕其中心的转速可达50 r/s，此时纽扣上距离中心1 cm处的点向心加速度大小约为（   ）

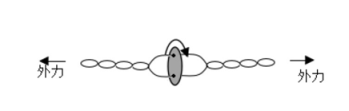
A．

10 m/s ^2

B．

100 m/s ^2

C．

1000 m/s ^2

D．

10 000 m/s ^2

我国研制并成功发射的“嫦娥二号”探测卫星，在距月球表面高度为h的轨道上做匀速圆周运动，运行的周期为T，若以R表示月球的半径，则

A．卫星运行时的线速度为

B．卫星运行时的向心加速度为

C．月球的第一宇宙速度为

D．物体在月球表面自由下落的加速度为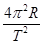

如图所示，长度为l的细绳上端固定在天花板上O点，下端栓这质量为m的小球。当把细绳拉直时，细绳与竖直线夹角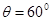，此时小球静止与光滑的水平面上。

（1）当球以角速度做圆锥摆运动时，细绳的张力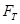为多大？水平面受到的压力N是多大？
（2）当球以角速度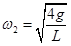做圆锥摆运动时，细绳的张力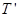为多大？水平面受到的压力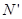是多大？

如图所示，无限宽广的匀强磁场分布在xoy平面内，x轴上下方磁场均垂直xoy 平面向里，x轴上方的磁场的磁感应强度为B，x轴下方的磁场的磁感应强度为4B/3。现有一质量为m，电量为-q带负电粒子以速度v₀从坐标原点O沿y方向进入上方磁场。在粒子运动过程中，与x轴交于若干点。不计粒子的重力。求：

（1）粒子在x轴上方磁场做匀速圆周运动半径r₁
（2）如把x轴上方运动的半周与x轴下方运动的半周称为一周期的话，则每经过一周期，在x轴上粒子右移的平均速度。
（3）在与x轴的所有交点中，粒子两次通过同一点的坐标位置。

如图所示，质量不计的轻质弹性杆P插入桌面上的小孔中，杆的另一端固定着一个质量为m的小球，今使小球在水平面内做半径为R的匀速圆周运动，角速度为ω。则下列说法正确的是（重力加速度为g）

A．球所受的合外力大小为

B．球所受的合外力大小为

C．球对杆作用力的大小为

D．球对杆作用力的大小为

如图所示，足够大的光滑绝缘水平面上有三个带电质点M、O、N，质点O恰能保持静止，质点M、N均围绕质点O做匀速圆周运动。已知质点M、N与质点O的距离分别为L₁、L₂。不计质点间的万有引力作用。下列说法中正确的是（    ）

A．质点M与质点N带有异种电荷

B．质点M与质点N的线速度相同

C．质点M与质点N的质量之比为

D．质点M与质点N所带电荷量之比为

小球以水平速度v进入一个水平放置的光滑的螺旋形轨道，若轨道半径逐渐减小，则(　　)．

A．球的向心加速度不断增大

B．球的角速度不断增大

C．球对轨道的压力不断增大

D．小球运动的周期不断增大