(如图所示,长为3L的轻杆可绕光滑水平转轴O转动,在杆两端分别固定质量均为m的球A、B,球A距轴O的距离为已知。现给系统一定能量,使杆和球在竖直平面内转动.当球B运动到最高点时,水平转轴O对杆的作用力恰好为零,忽略空气阻力,已知重力加速度为g,则球B在最高点时,下列说法正确的是
A.球B的速度为零
B.球B的速度为
C.球A的速度大于
D.杆对球B的弹力方向竖直向上
在街头的理发店门口,常可以看到有这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉.如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L=10cm,圆筒沿逆时针方向(从俯视方向看),以2转/秒的转速匀速转动,我们感觉到的升降方向和速度大小分别为( )
| A.向上 10cm/s | B.向上 20cm/s | C.向下 10cm/s | D.向下 20cm/s |
如图所示,小物块A与圆盘保持相对静止,跟着圆盘一起作匀速圆周运动,则下列关于A的受力情况说法正确的是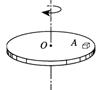
| A.受重力、支持力 |
| B.受重力、支持力和指向圆心的摩擦力 |
| C.受重力、支持力、摩擦力和向心力 |
| D.受重力、支持力和与运动方向相同的摩擦力 |
如图所示,两个小球用长度不等的细线悬挂在天花板上的同一点,并在同一水平面内做匀速圆周运动,则下列说法正确的是( )
| A.两球运动的周期一定相同 |
| B.两球运动的线速度大小一定相等 |
| C.两球运动的角速度大小一定相等 |
| D.两球运动的向心加速度大小一定相等 |
如图所示,a、b两颗人造地球卫星分别在半径不同的轨道上绕地球作匀速圆周运动,则下列说法正确的是( )
| A.a的周期小于b的周期 | B.a的动能大于b的动能 |
| C.a的势能小于b的势能 | D.a的加速度大于b的加速度 |
下列说法正确的是( )
| A.竖直平面内做匀速圆周运动的物体,其合外力可能不指向圆心 |
| B.匀速直线运动和自由落体运动的合运动一定是曲线运动 |
| C.物体竖直向上做匀加速直线运动时,物体受到的重力将变大 |
| D.火车超过限定速度转弯时,车轮轮缘将挤压铁轨的外轨 |
如图所示为圆锥摆示意图,用长为L的细绳一端固定,另一端系着一个小球,使小球在水平面内做匀速圆周运动,细绳与竖直方向的夹角为θ,不计空气阻力,重力加速度为g,则小球的角速度大小为( )
A. |
B. |
C. |
D. |
质量为m的物体沿半径为R的半球形金属球壳滑到最低点时的速度大小为v,如右图所示,若物体与球壳间的动摩擦因数为μ,则物体在最低点时 ( )
A.向心加速度为
B.向心力为
c.摩擦力为
D.对球壳的压力为
球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如右图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么 ( )
| A.球A受到的向心力大于B受到的向心力 |
| B.球A转动的半径是球B转动半径的一半 |
| C.当A球质量增大时,球A向外运动 |
| D.当ω增大时,球B向外运动 |
关于圆周运动,下列说法正确的是
| A.匀速圆周运动是匀速运动 |
| B.匀速圆周运动是变速运动 |
| C.匀速圆周运动是变加速运动 |
| D.做圆周运动的物体加速度一定始终指向圆心 |
下列关于圆周运动的说法中,正确的是( )
| A.物体受到的合外力必须指向圆心才可能做圆周运动 |
| B.物体的实际加速度就是向心加速度 |
| C.在匀速圆周运动中,物体因为速率不变所以加速度为零 |
| D.在匀速圆周运动中,物体沿切线方向无加速度 |
如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
| A.球A的角速度一定小于球B的角速度 |
| B.球A的线速度一定大于球B的线速度 |
| C.球A的运动周期一定小于球B的运动周期 |
| D.球A对筒壁的压力等于球B对筒壁的压力 |
一质点做匀速圆周运动时,圆的半径为r,周期为4 s,那么1 s内质点的位移大小和路程分别是 ( ).
A.r和 |
B. 和 和 |
C. r和 r和 r r |
D. r和 r和 |
以下有关物理学概念或物理学史说法正确的有( )
| A.行星绕恒星运动轨道为圆形,则它运动的周期平方与轨道半径的三次方之比k为常数,此常数的大小与恒星的质量和行星的速度有关 |
| B.匀速圆周运动是速度大小不变的匀变速曲线运动,速度方向始终为运动轨迹该点的切线方向 |
| C.牛顿发现的万有引力定律,卡文迪许用实验方法测出万有引力恒量的数值,从而使万有引力定律有了真正的实用价值 |
| D.奥斯特发现了电与磁间的关系,即电流的周围存在着磁场;同时他通过实验发现了磁也能产生电,即电磁感应现象 |
物体在做匀速圆周运动的过程中,保持不变的物理量为( )
| A.线速度 | B.角速度 | C.向心力 | D.向心加速度 |