如图所示,固定在竖直平面的光滑绝缘圆环处于匀强电场中,场强方向与圆环平面平行且与水平方向成30°,环上与圆心O等高的A点套有一个质量为m,电荷量为+q的小球恰好处于平衡状态.(重力加速度为g),求: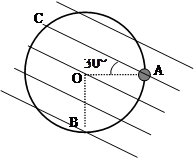
(1)匀强电场的场强大小
(2)某时刻突然将电场方向变为竖直向下,场强大小不变,小球滑到最低点B时对环的压力大小
在2012年元旦晚会上,河北杂技团表演了杂技“大球扛杆”。在一个大球上竖立一根直杆,演员在直杆上做了精彩表演。如图所示.假设直杆与大球之间有一压力传感器.一个质量为50kg的演员匀速向上运动时传感器显示压力为600N;演员从直杆最上端由静止开始向下匀加速运动一段时间后又匀减速运动一段时间速度减小到零,静止在距直杆底端1/3处。已知在演员向下运动时传感器显示的最大压力为700N,最小压力为500N,直杆长度为12m,g取10m/s2。求:
(1)直杆的质量;
(2)演员下降过程中加速、减速的加速度;
(3)演员向下运动的平均速度。
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ.现有质量为m的小物体从距D点为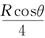 的高处无初速释放,已知物体恰能从D点进入圆轨道,求:
的高处无初速释放,已知物体恰能从D点进入圆轨道,求: 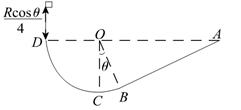
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物块与斜面间的动摩擦因数μ=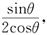 则小物体在斜面上通过的总路程为多少?
则小物体在斜面上通过的总路程为多少?
(3)在(2)的条件下,当小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?
如图所示,一个质量为M的人,站在台秤上,一长为R的悬线一端系一个质量为m的小球,手拿悬线另一端,小球绕悬线另一端点在竖直平面内做圆周运动,不计空气阻力,重力加速度为g,求: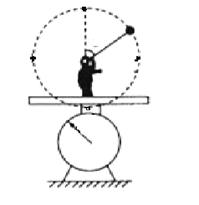
(1)若小球恰能通过圆轨道最高点,求小球通过最低点时对绳子拉力的大小。
(2)若小球恰能在竖直平面内做圆周运动,求台秤示数的最小值。
滑雪是人们喜爱的一项体育运动.一滑雪坡由AB和BC组成,AB是倾角为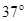 的斜坡,BC是半径为
的斜坡,BC是半径为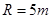 的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差为
的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差为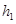 ,竖直台阶CD高度差为
,竖直台阶CD高度差为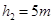 ,台阶底端与倾角为
,台阶底端与倾角为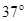 斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下以
斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下以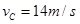 ,通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,
,通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,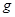 取10m/s2,sin37°=0.6,cos37°=0.8).求:
取10m/s2,sin37°=0.6,cos37°=0.8).求: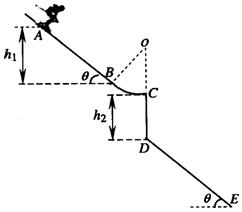
(1)AB竖直方向的高度差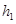 ;
;
(2)运动员刚过B点瞬间轨道受到的压力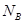 ?
?
(3)运动员在空中飞行的时间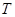 ?
?
如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v。水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R="2.5" m的圆截去了左上角l270的圆弧,CB为其竖直直径,(sin530="0.8" cos530=0.6,重力加速度g取10m/s2)求: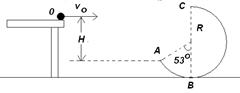
(1) 小球经过C点的速度大小;
(2) 小球运动到轨道最低点B时小球对轨道的压力大小;
(3) 平台末端O点到A点的竖直高度H。
如图所示,小球被轻质细绳系住斜吊着放在光滑斜面上,小球与斜面均处于静止状态,设小球质量m=2 kg,斜面倾角α=30°,细绳与竖直方向夹角θ=30°,光滑斜面体的质量M=3 kg,置于粗糙水平面上.(g取10 m/s2)求: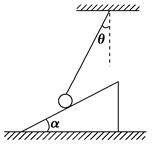
(1)细绳对小球拉力的大小;
(2)地面对斜面体的摩擦力的大小和方向.
超市一送水员用双轮小车运送桶装矿泉水.装运完毕,如图所示,在拉运过程中保持图示角度不变,不计桶与小车之间摩擦力的影响.求:
(1)小车静止时,桶对小车两侧轨道的压力大小之比NA:NB
(2)若送货员以5m/s2的恒定加速度由静止开始向右拉动小车,请问这一过程中,桶对小车两侧轨道的压力大小之比NA:NB.(g= 10m/s2,结果可用根号表示)
如图所示,质量M=400g的劈形木块B上叠放一木块A,A的质量为m=200g。A、B一起放在斜面上,斜面倾角θ=37°,B的上表面呈水平,B与斜面之间及B与A之间的动摩擦因数均为μ=0.2。当B受到一个F=5.76N的沿斜面向上的作用力时,A相对B静止,并一起沿斜面向上运动。
(sin37°=0.6,cos37°=0.8,g=10m/s2)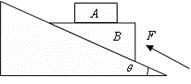
求:(1)B的加速度大小;
(2)A受到的摩擦力及A对B的压力大小。
如图所示,表面光滑的球A半径为10 cm,用长L=50 cm的悬线挂在竖直墙上,球与墙之间夹着物体B,其厚20 cm,重12 N,与墙之间的动摩擦因数μ=0.2.物块B在未脱离球A时沿墙匀速下滑,试求:
(1)球A受的重力;
(2)球A对物块B的压力.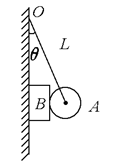
如图所示,一半径R=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点)。在圆盘直径 DE 的正上方平行放置一水平滑道 BC ,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度 h =" 1.25" m。AB为一竖直面内的光滑四分之一圆弧轨道,半径r=0.45m,且与水平滑道相切与B点。一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过B点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数 =0.2。(取g=10m/
=0.2。(取g=10m/ )
)
求
(1)滑块到达B点时对轨道的压力
(2)水平滑道 BC的长度;
(3)圆盘转动的角速度ω应满足的条件。
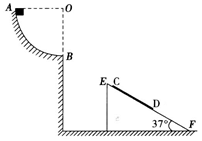
如图所示,AB段为一半径R=0.2m的光滑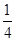 圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为
圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为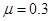 (g取
(g取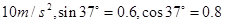 ),
),
求:(1)物块到达B点时对圆弧轨道压力的大小;
(2)物块做平抛运动的时间;
(3)若下滑过程中某时刻物块和木板达到共同速度,则这个速度为多大?(木板足够长)
如图所示,ABDO是固定在竖直平面内的轨道,AB是一光滑弧形轨道,OA处于水平位置,BDO是半径为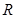 的粗糙半圆轨道,AB和BDO相切于B点.质量为
的粗糙半圆轨道,AB和BDO相切于B点.质量为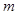 的小球P(可视作质点)从A点的正上方距OA所在水平面高
的小球P(可视作质点)从A点的正上方距OA所在水平面高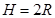 处自由落下,沿竖直平面内的轨道运动恰好通过O点.已知重力加速度为
处自由落下,沿竖直平面内的轨道运动恰好通过O点.已知重力加速度为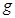 。求:
。求:
(1)小球进入BDO轨道时对B点的压力;
(2)球经过BDO轨道克服摩擦力做功.
如图所示,摩托车做腾跃特技表演,沿曲面冲上高0.8m顶部水平高台,接着以v=3m/s水平速度离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑。A、B为圆弧两端点,其连线水平。已知圆弧半径为R=1.0m,人和车的总质量为180kg,特技表演的全过程中,阻力忽略不计。(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)。求:
(1)从平台飞出到A点,人和车运动的水平距离s;
(2)从平台飞出到达A点时速度及圆弧对应圆心角θ;
(3)人和车运动到达圆弧轨道A点时对轨道的压力;
(4)人和车运动到圆弧轨道最低点O速度vo= m/s此时对轨道的压力。
m/s此时对轨道的压力。