如图所示,小球A从半径为R=0.8 m的1/4光滑圆弧轨道的上端点以v0=3 m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10 m/s2,求:
(1)小球A刚滑上水平面的速度.
(2)A和B的质量之比.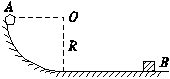
关于机械能守恒定律的适用条件,下列说法中正确的是:
| A.只要有重力和弹力作用时,机械能一定守恒 |
| B.当有其他外力作用时,只要合外力为零,机械能一定守恒 |
| C.当有其他外力作用时,只有重力做功,机械能一定守恒 |
| D.物体只受重力作用的运动,机械能一定守恒 |
如图所示,质量是20kg的小车,在一个与斜面平行的200N的拉力作用下,由静止开始前进了3m,斜面的倾角为300,小车与斜面间的摩擦力忽略不计.求这一过程物体的重力势能增加了多少?物体的动能增加了多少? 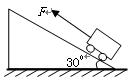
质量为m的小球,从离桌面H高处由静止下落,桌面离地面高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别是: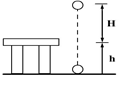
| A.mgh,减少mg(H—h) | B.mgh,增加mg(H+h) |
| C.-mgh,增加mg(H—h) | D.-mgh,减少mg(H+h) |
甲物体在水平外力作用下静止在乙物体上,乙物体静止在水平面上。现增大外力F两物体仍然静止。则下列说法正确的是: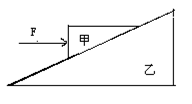
| A.乙对甲的摩擦力一定增大。 |
| B.乙对甲的摩擦力方向一定沿斜面向上。 |
| C.乙对地面的摩擦力一定增大。 |
| D.乙对地面的压力一定增大。 |
以初速度v0竖直向上抛出一个质量为m的小球,小球运动过程中所受阻力f的大小不变,上升的最大高度为h,则抛出过程中,人手对小球做的功为(设急速抛出):( )
A.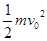 |
B.mgh | C.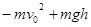 |
D.mgh+fh |
一质量为M="2.0" kg的小物块随足够长的水平传送带一起运动,被一水平向左飞来的子弹击中并从物块中穿过,如图(一)所示.地面观察者纪录了小物块被击中后的速度随时间的变化关系如图(二)所示(图中取向右运动的方向为正方向).已知传送带的速度保持不变,g取10 m/s2.
(1)指出小物块随传送带一起运动速度v的方向及大小,并说明理由;
(2)计算物块与传送带间的动摩擦因数μ;
(3)计算传送带总共对外做了多少功?系统有多少能量转化为热能?
长木板A放在光滑的水平面上,质量为m=2 kg的另一物体B以水平速度v0=2 m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图9所示,则下列说法正确的是( )
A.木板获得的动能为2 J B.系统损失的机械能为4 J
C.木板A的最小长度为1 m D.A、B间的动摩擦因数为0.1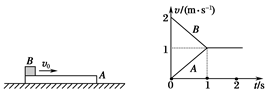
如图所示,长木板静止在光滑水平面上,其左端放有可视为质点的小木块,小木块在水平恒力F作用下,经时间t从长木板左端被拉到右端.已知水平恒力F=5N,小木块质量m=1kg,长木板质量M=2kg,木板长度L=1m,木板与小木块间的动摩擦因数μ=0.2,重力加速度g=10m/s2.求:
(1)F作用的时间t;
(2)小木块克服摩擦力所做的功.
一质量为m的滑雪者从A点由静止沿粗糙曲面滑下,到B点后水平飞离B点.空间几何尺寸如图所示,滑雪者从B点开始做平抛运动的水平距离为S,求滑雪者从A点到B点的过程中摩擦力对滑雪者做的功。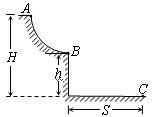
如图所示,小球从A点以初速度vo沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点。下列说法中正确的是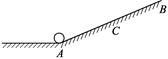
| A.小球从A出发到返回A的过程中,位移为零,外力做功为零 |
| B.小球从A到C与从C到B的过程,减少的动能相等 |
| C.小球从A到C与从C到B的过程,速度的变化率相等 |
| D.小球从A到C与从C到B的过程,损失的机械能相等 |
两名质量相等的滑冰人甲和乙都静止在光滑的水平冰面上.现在,其中一人向另一个人抛出一个篮球,另一人接球后再抛回.如此反复进行几次后,甲和乙最后的速率关系是( )
| A.若甲最先抛球,则一定是v甲>v乙 |
| B.若乙最后接球,则一定是v甲>v乙 |
| C.只有甲先抛球,乙最后接球,才有v甲>v乙[来源:Z§xx§k.Com] |
| D.无论怎样抛球和接球,都是v甲>v乙 |
关于弹性势能,下列说法正确的是 ( )
| A.弹性势能与物体的形变量有关 | B.弹性势能与物体的形变量无关 |
| C.物体运动的速度越大,弹性势能越大 | D.物体运动的速度越大,弹性势能越小 |
关于重力势能和重力做功的说法中正确的是:
| A.重力做负功,物体的重力势能一定增加 |
| B.地面上物体的重力势能一定为零 |
| C.只要有力对物体做功,该物体的重力势能就一定增加 |
| D.质量较大的物体,其重力势能也一定较大 |