如图所示,一个重60 N的物体置于水平面上,当用一个 的力竖直向上拉物体时,物体所受的合力为( )
的力竖直向上拉物体时,物体所受的合力为( )

| A.0N |
| B.40N,方向竖直向下 |
| C.40N,方向竖直向上 |
| D.80N,方向竖直向上 |
在如下所示的A、B、C、D四图中,滑轮本身的重力忽略不计,滑轮的轴O安装在一根轻木杆P上,一根轻绳ab绕过滑轮,a端固定在墙上,b端下面挂一个质量都是m的重物,当滑轮和重物都静止不动时,A、C、D图中杆P与竖直方向夹角均为θ,图B中杆P在竖直方向上,假设A、B、C、D四图中滑轮受到木杆弹力的大小依次为FA、FB、FC、FD,则以下判断中正确的是
A.FA=FB= FC=FD B.FD>FA=FB>FC
C.FA= FC=FD>FB D.FC>FA=FB>FD
如图所示,在光滑的水平面上有一质量为M、倾角为θ的光滑斜面体,它的斜面上有一质量为m的物块沿斜面下滑。关于物块下滑过程中对斜面压力大小的解答,有如下四个表达式。要判断这四个表达式是否合理,你可以不必进行复杂的计算,而根据所学的物理知识和物理方法进行分析,从而判断解的合理性或正确性。根据你的判断,下述表达式中可能正确的是( )
A. |
B. |
C. |
D. |
如图所示,A、B为竖直墙壁上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆。转轴C在AB中点D的正下方,AOB在同一水平面上。∠AOB=90º,∠COD=60º。若在O点处用轻绳悬挂一个质量为m的物体,则平衡后绳AO所受拉力的大小为( )
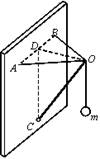
A.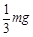 B.
B.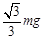 C.
C. D.
D.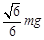
两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止与水平地面上,如图所示,不计摩擦力,A对绳的作用力的大小与地面对A的作用的大小分别为
| A.mg,Mg |
| B.mg,(M-m)g |
| C.(M-m)g,Mg |
| D.(M+-m)g,(M-m)g |
如图所示,两个完全相同的光滑球的质量均为m,放在竖直挡板和倾角为α的固定斜面间.若缓慢转动挡板至与斜面垂直,在此过程中

A.A球对斜面的压力逐渐减小 B.B球对挡板的压力逐渐减小
C.B球对斜面的压力逐渐减小 D.A、B两球间的弹力增大
有三个大小分别为5N、6N和8N的共点力,它们的合力最大值和最小值分别为( )
| A.9N和0N | B.9N和3N | C.19N和0N | D.19N和3N |
如图舰载机保持牵引力F大小不变在匀速航行的航母上降落时受到阻拦而静止,此时阻拦索夹角 ,空气阻力和甲板阻力不计,则阻拦索承受的张力大小为
,空气阻力和甲板阻力不计,则阻拦索承受的张力大小为 
A. |
B.F | C. F F |
D.2F |
如图,用OA、OB两根轻绳将物体悬于两竖直墙之间,开始时OB 绳水平。现保持O点位置不变,改变OB绳长使绳端由B点缓慢上移至B′点,此时OB′与OA之间的夹角θ<90°。设此过程中OA、OB的拉力分别为FOA、FOB,下列说法正确的是( )
A.FOA逐渐增大 B.FOA逐渐减小 C.FOB逐渐增大 D.FOB逐渐减小
物体静止在水平面上,今对物体施加一个与水平方向成θ角的斜向上的拉力F,保持θ角不变,使F从零开始逐渐增大的过程中,物体始终未离开水平面,在此过程中物体受到的摩擦力将( )
| A.逐渐增大 | B.逐渐减小 |
| C.先逐渐增大后逐渐减小 | D.先逐渐减小后逐渐增大 |
如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接。倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,下列说法正确的是( )

A.AB之间杆的拉力大小为
B.C球的加速度沿斜面向下,大小为g
C.A、B两个小球的加速度均沿斜面向上,大小均为
D.A球的受力情况未变,加速度为零
如图所示,有一竖直放置的“T”形架,表面光滑,滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻绳相连,A、B质量相等,且可看做质点.开始时细绳水平伸直,A、B静止.由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v时,则A的速度为( )

A.v B. v C.
v C. v D.
v D. v
v
如图所示,三角形ABC由三根光滑的杆构成三角形框架,竖直固定放置, ,
, ,质量均为m的A.b两个小球分别套在AB.AC杆上,两球间由细线连接,两球静止时,细线与AB杆成
,质量均为m的A.b两个小球分别套在AB.AC杆上,两球间由细线连接,两球静止时,细线与AB杆成 角,则下列说法中正确的是( )
角,则下列说法中正确的是( )

A.
B.细线受到的拉力大小为mg
C.A.b两小球对杆的压力大小之比为
D.细线受到的拉力大小为
如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )

| A.f1=μ1 Mg f2=μ1 mg |
| B.f1=μ1(M+m)g f2=μ1 mg |
| C.f1=μ1Mg f2=μ2mg |
| D.f1=μ1(M+m)g f2=μ2 mg |