如图所示,开口向下的“┍┑”形框架,两侧竖直杆光滑固定,上面水平横杆中点固定一定滑轮,两侧杆上套着的两滑块用轻绳绕过定滑轮相连,并处于静止状态,此时连接滑块A的绳与水平方向夹角为θ,连接滑块B的绳与水平方向的夹角为2θ,则A、B两滑块的质量之比为( )
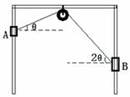
A.2sinθ:1 B.2cosθ:1 C.1:2cosθ D.1:2sinθ
关于3N、4N、6N三个共点力,下面说法正确的是( )
| A.它们的合力可能为零 | B.它们的合力的最大值为13N |
| C.它们的合力的最小值为1N | D.以上说法均不正确 |
某同学为探究求合力的方法,做了如图所示的实验.ABCD为竖直平板,E、F两处固定了摩擦不计的轻质滑轮,滑轮的轴保持水平,所用绳子的质量可不计.第一次实验中,当装置平衡时,绳子的结点在O处,拉力的方向和钩码的位置如图所示.第二次实验时,仅把右侧滑轮的位置移动到图中的G点,待稳定后,∠EOF将 (填“变大”、“变小”或“不变”),绳子结点O的位置将

| A.竖直向下移动 |
| B.水平向右移动 |
| C.沿EO方向移动 |
| D.沿FO方向移动. |
如图所示,轻绳两端分别与A.C两物体相连, ,物体A.B.C之间及C与地面间的动摩擦力因数均为μ=0.3,轻绳与滑轮间的摩擦可忽略不计,设最大静摩擦力等于滑动摩擦力,若要用力将C物体拉动,则作用在C物体上水平向左的拉力最小为(取
,物体A.B.C之间及C与地面间的动摩擦力因数均为μ=0.3,轻绳与滑轮间的摩擦可忽略不计,设最大静摩擦力等于滑动摩擦力,若要用力将C物体拉动,则作用在C物体上水平向左的拉力最小为(取 )
)

A.48N B.42N C.36N D.24N
如图所示,一个菱形框架绕着过对角线的竖直轴匀速转动,在两条边上各有一个质量相等的小球套在上面,整个过程小球相对框架没有发生滑动,A与B到轴的距离相等,则下列说法正确的是
A.框架对A的弹力方向可能垂直框架向下
B.框架对B的弹力方向只能垂直框架向上
C.A与框架间可能没有摩擦力
D.A、B两球所受的合力大小相等
两个大小相等的共点力F1、F2,当它们间夹角为90°时合力大小为20N,则它们间夹角为120°时,合力大小为( )
| A.40N | B. |
C. |
D. |
如图所示,质量为m的小球,与三根相同的轻弹簧相连.静止时,弹簧c沿竖直方向,相邻两弹簧轴线间的夹角均为120°.已知弹簧a、b对质点的作用力大小均为F,则弹簧c对小球的作用力大小
| A.可能为F ,也可能为F+mg |
| B.可能为F ,一定不可能为F+mg |
| C.可能为F-mg,一定不可能为mg-F |
| D.可能为mg-F,也可能为F-mg |
如图所示,用一小车通过轻绳提升一滑块,滑块沿竖直光滑杆上升,某一时刻,两段绳恰好垂直,且拴在小车一端的绳与水平方向的夹角为θ,此时小车的速度为 ,则此时滑块竖直上升的速度为( )
,则此时滑块竖直上升的速度为( )

A. |
B. |
C. |
D. |
如图所示,重力为G的质点M,与三根劲度系数相同的螺旋弹簧A.B.C相连,C处于竖直方向,静止时,相邻弹簧间的夹角均为 ,已知弹簧A和B对质点的作用力的大小均为2G,则弹簧C对质点的作用力大小可能为( )
,已知弹簧A和B对质点的作用力的大小均为2G,则弹簧C对质点的作用力大小可能为( )

A.2G B.G C.0 D.3G
将10N的力分解为两个分力F1、F2,F1、F2的值不可能是下列的哪一组
| A.F1=6N,F2=3N | B.F1=12N,F2=3N |
| C.F1=F2=10N | D.F1=F2=20N |
如图,老鹰沿虚线MN 斜向下减速俯冲的过程中,空气对老鹰的作用力可能是图中的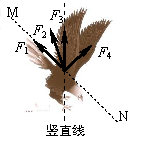
| A.F1 |
| B.F2 |
| C.F3 |
| D.F4 |
如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大的拉力为120N,而BC绳能承受的最大的拉力为80N,物体最大重力不能超过多少
A.100 N N |
B.160N |
C.80 N N |
D.100N |
有三个大小分别为5N、6N和8N的共点力,它们的合力最大值和最小值分别为( )
| A.9N和0N | B.9N和3N | C.19N和0N | D.19N和3N |