一物体受到三个共面共点力F1、F2、F3的作用,三力的矢量关系如图所示(小方格边长相等),则下列说法正确的是 ( )

| A.三力的合力有最大值F1+F2+F3,方向不确定 |
| B.三力的合力有唯一值3F3,方向与F3同向 |
| C.三力的合力有唯一值2F3,方向与F3同向 |
| D.由题给条件无法求出合力大小 |
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点。第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1;第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力为大小T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是
| A.第一个过程中,拉力F在逐渐变大,且最大值一定大于F′ |
| B.两个过程中,轻绳的张力均变大 |
C. , , |
| D.第二个过程中,重力和水平恒力F′的合力的功率先增加后减小 |
在完成《互成角度的两个共点力的合成》实验中.如图所示,用两只弹簧秤把结点拉到某一位置O,固定左边的测力计不动,移动右边的测力计,使橡皮筋节点仍在O点.那么,右边的测力计能否再有新的位置( )

| A.一定没有别的位置 |
| B.一定还有一个位置可以 |
| C.可能没有了,也可能有一个位置 |
| D.有无穷多的可能位置 |
如图所示,将完全相同的两小球A、B用长L=0.8 m的细绳悬于以v=4 m/s向左匀速运动的小车顶部,两球分别与小车前后壁接触.由于某种原因,小车突然停止,此时悬线中张力之比FTA∶FTB为 ( )

A.1∶1 B.1∶2 C.1∶3 D.1∶4
两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止与水平地面上,如图所示,不计摩擦力,A对绳的作用力的大小与地面对A的作用的大小分别为
| A.mg,Mg |
| B.mg,(M-m)g |
| C.(M-m)g,Mg |
| D.(M+-m)g,(M-m)g |
如图所示,物体A、B、C放在光滑水平面上用细线a、b连接,力F作用在A上,使三物体一起在水平面上运动,若在B上放一小物体D,D随B一起运动,且拉力,保持不变,那么加上物体D后两绳中拉力的变化是

A.Ta不变 B.Tb增大 C.Ta变小 D.Tb变小
如图所示为质量均可忽略的轻绳与轻杆组成系统,轻杆A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),轻杆B端吊一重物G.现将绳的一端拴在杆的B端,用拉力F将B端缓慢向上拉(均未断),在AB杆转到竖直方向前,以下分析正确的是( )

| A.绳子受到的拉力越来越大 |
| B.AB杆受到的压力越来越小 |
| C.AB杆受到的压力越来越大 |
| D.绳子受到的拉力越来越小 |
如图所示,A.B两物块静止叠放在水平地面上,A与B.B与地面间均粗糙。现对A施加一水平拉力F使得A.B均运动且A.B相对运动,则物块B受力个数为( )

A.4个 B.5个 C.6个 D.7个
将10N的力分解为两个分力F1、F2,F1、F2的值不可能是下列的哪一组
| A.F1=6N,F2=3N | B.F1=12N,F2=3N |
| C.F1=F2=10N | D.F1=F2=20N |
如图,老鹰沿虚线MN 斜向下减速俯冲的过程中,空气对老鹰的作用力可能是图中的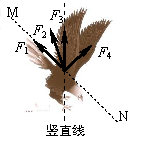
| A.F1 |
| B.F2 |
| C.F3 |
| D.F4 |
如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大的拉力为120N,而BC绳能承受的最大的拉力为80N,物体最大重力不能超过多少
A.100 N N |
B.160N |
C.80 N N |
D.100N |
有三个大小分别为5N、6N和8N的共点力,它们的合力最大值和最小值分别为( )
| A.9N和0N | B.9N和3N | C.19N和0N | D.19N和3N |
如图所示,物体A和B的重力分别为10N和3N,不计弹簧秤和细线的重力和一切摩擦,则弹簧秤所受的合力和弹簧秤的读数为
| A.0N 13N | B.7N 3N |
| C.0N 3N | D.7N 13N |