物体以初速度
竖直上抛，经3s到达最高点，空气阻力不计，g取
，则下列说法正确的是（ ）
| A．物体上升的最大高度为45m |
| B．物体速度改变量的大小为30m/s，方向竖直向上 |
| C．物体在第1s内、第2s内，第3s内的平均速度之比为5:3:1 |
| D．物体在1s内、2s内，3s内的平均速度之比为9:4:1 |
从地面以大小为v1的初速度竖直向上抛出一个皮球，经过时间t皮球落回地面，落地时皮球的速度大小为v2.已知皮球在运动过程中受到空气阻力的大小与速度的大小成正比，重力加速度大小为g.下面给出时间t的四个表达式中只有一个是合理的．你可能不会求解t，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断．根据你的判断，你认为t的合理表达式应为
A．t＝ |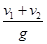
B．t＝ |
C．t＝ |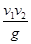
D． |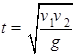
以不同初速度将两个物体同时竖直向上抛出并开始计时，一个物体所受空气阻力可忽略，另一个物体所受空气阻力大小与物体速率成正比。下列用虚线和实线描述两物体运动的v-t图象可能正确的是
球A以初速度
从地面上一点竖直向上抛出，经过一段时间
后又以初速度
将球B从同一点竖直向上抛出（忽略空气阻力），为了使两球能在空中相遇， 取值范围正确的是（ ）。
| A．3S﹤﹤ 4S |
B．0 ﹤﹤6S |
| C．2S﹤﹤8S |
D．0﹤﹤8S |
竖直上抛一个小球，从抛出到落回抛出点的过程中，它的速度、重力势能、位移和加速度随时间变化的函数图像（如图所示）中错误的是（不计空气阻力、规定竖直向下为正方向，图中曲线均为抛物线、规定抛出点所在水平面为零势能参考面）
竖直上抛一个小球，从抛出到落回抛出点的过程中，它的速度v、重力势能E、位移x和加速度a随时间t变化的函数图像（如图所示）中错误的是（不计空气阻力、规定竖直向下为正方向，图中曲线均为抛物线、规定抛出点所在水平面为零势能参考面）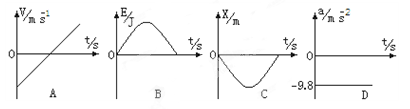
每隔0.3s从同一高度抛出一个小球，小球做初速为6m/s的竖直上抛运动，设它们在空中不相碰。第一个小球在抛出点以上能遇到的小球数为（取g＝10m/s2）（ ）
| A．三个 | B．四个 | C．五个 | D．六个 |
以不同初速度将两个物体同时竖直向上抛出并开始计时，一个物体所受空气阻力可忽略，另一物体所受空气阻力大小与物体速率成正比，下列用虚线和实线描述两物体运动的
图像可能正确的是（）
| A． |
|
B． |
|
| C． |
|
D． |
|
在地质、地震、勘探、气象和地球物理等领域的研究中，需要精确的重力加速度g值，g值可由实验精确测定．近年来测g值的一种方法叫“对称自由下落法”，它是将测g值归于测长度和时间，以稳定的氦氖激光的波长为长度标准，用光学干涉的方法测距离，以铷原子钟或其他手段测时间，此方法能将g值测得很准．具体做法是：将真空长直管沿竖直方向放置，自其中的O点向上抛小球，从抛出小球至小球又落回抛出点的时间为T2；小球在运动过程中经过比O点高H的P点，小球离开P点至又回到P点所用的时间为T1.由T1、T2和H的值可求得g等于( )
A． |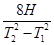
B． |
C． |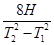
D． |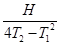
如图所示，小球B放在真空容器A内，球B的直径恰好等于正方体A的边长，将它们以初速度V0竖直向上抛出，下列说法中正确的是( )
| A．若不计空气阻力，上升过程中，A对B有向上的支持力 |
| B．若考虑空气阻力，上升过程中，A对B的压力向下 |
| C．若考虑空气阻力，下落过程中，B对A的压力向上 |
| D．若不计空气阻力，下落过程中，B对A没有压力 |
从地面以一定的速度竖直向上抛出一小球，以抛出点为计时起点，小球上升到最高点的时刻为t1，下落到抛出点的时刻为t2。若空气阻力的大小恒定，则在下图中能正确表示被抛出物体的速率v随时间t的变化关系的图线是 （ ）
在离地高h处，沿竖直方向同时向上和向下抛出两个小球，它们的初速度大小均为v，不计空气阻力，两球落地的时间差为
A． |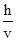
B． |
C． |
D． |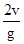
如图所示，a、b两小球静止在同一竖直线上，mb>ma。两球间用一轻质弹簧
相连，开始时弹簧处于原长状态。现同时以相同的初速度v0竖直向上抛射出
两球，两球在运动过程中所受空气阻力忽略不计，则（ ）
| A．两球上升过程中，弹簧的长度将越来越大，直至两球再次达到相同速度 |
| B．两球下降过程中，弹簧的长度将越来越小，直至两球再次达到相同速度 |
| C．无论两球上升还是下降，弹簧均处于原长 |
| D．上升过程时弹簧的长度将大于下降过程时弹簧的长度 |
粤公网安备 44130202000953号