虚线MN下方有竖直向上的匀强电场,场强大小E=2×103V/m,MN上方有一竖直长为L=0.5m的轻质绝缘杆,杆的上下两端分别固定一带电小球A、B(可看成质点),质量均为m=0.01kg,A带电量为 ;B带电量
;B带电量 ,B到MN的距离h=0.05m。现将杆由静止释放(g取10m/s2),求:
,B到MN的距离h=0.05m。现将杆由静止释放(g取10m/s2),求:
(1)小球B在匀强电场中,而A还未进入电场时,两小球的加速度大小。
(2)从开始运动到A刚要进入匀强电场过程的时间。
如图所示,当K1、K2均闭合时,一质量为m、带电荷量为q的液滴,静止在电容器的两平行金属板A.B间,现保持K1闭合,将K2断开,然后将B板向下平移一段距离,则下列说法正确的是( )

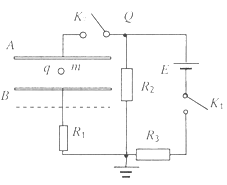
A.电容器的电容变小
B.A板的电势比电路中Q点的电势高
C.液滴向下加速运动
D.液滴的电势能减小
如图所示,水平虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B。一带负电微粒自离EF为h的高处自由下落,从B点进入场区,沿虚线BCD做匀速圆周运动,从D点射出.已知重力加速度为g,下列说法正确的是:( )
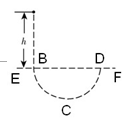
A.电场强度的方向竖直向上
B.微粒做圆周运动的半径为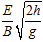
C.从B点运动到D点的过程中微粒的电势能先减小后增大
D.从B点运动到D点的过程中微粒的电势能和重力势能相加之和先增大后减小
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0=0.4 s,但饮酒会导致反应时间延长.在某次试验中,志愿者少量饮酒后驾车以v0=72 km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39 m,减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动.(g="10" m/s2)求:
(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者的反应时间比一般人增加了多少;
为了提高自行车夜间行驶的安全性,小明同学设计了一种“闪烁”装置。如图所示,自行车后轮由半径 的金属内圈、半径
的金属内圈、半径 的金属外圈和绝缘幅条构成.后轮的内、外圈之间等间隔地接有4跟金属条,每根金属条的中间均串联有一电阻值为
的金属外圈和绝缘幅条构成.后轮的内、外圈之间等间隔地接有4跟金属条,每根金属条的中间均串联有一电阻值为 的小灯泡.在支架上装有磁铁,形成了磁感应强度
的小灯泡.在支架上装有磁铁,形成了磁感应强度 、方向垂直纸面向外的“扇形”匀强磁场,其内半径为
、方向垂直纸面向外的“扇形”匀强磁场,其内半径为 、外半径为
、外半径为 、张角
、张角 .后轮以角速度
.后轮以角速度 ,相对转轴转动.若不计其它电阻,忽略磁场的边缘效应.
,相对转轴转动.若不计其它电阻,忽略磁场的边缘效应.
(1)当金属条 进入“扇形”磁场时,求感应电动势E,并指出ab上的电流方向;
进入“扇形”磁场时,求感应电动势E,并指出ab上的电流方向;
(2)当金属条 进入“扇形”磁场时,画出“闪烁”装置的电路图;
进入“扇形”磁场时,画出“闪烁”装置的电路图;
(3)从金属条 进入“扇形”磁场时开始,经计算画出轮子一圈过程中,内圈与外圈之间电势差
进入“扇形”磁场时开始,经计算画出轮子一圈过程中,内圈与外圈之间电势差 随时间
随时间 变化的
变化的 图象;
图象;
如图所示,质量 ,电阻
,电阻 ,长度
,长度 的导体棒
的导体棒 横放在U型金属框架上.框架质量
横放在U型金属框架上.框架质量 ,放在绝缘水平面上,与水平面间的动摩擦因数
,放在绝缘水平面上,与水平面间的动摩擦因数 ,相距
,相距 的
的 相互平行,电阻不计且足够长.电阻
相互平行,电阻不计且足够长.电阻 的
的 垂直于
垂直于 .整个装置处于竖直向上的匀强磁场中,磁感应强度
.整个装置处于竖直向上的匀强磁场中,磁感应强度 .垂直于
.垂直于 施加
施加 的水平恒力,
的水平恒力, 从静止开始无摩擦地运动,始终与
从静止开始无摩擦地运动,始终与 保持良好接触.当
保持良好接触.当 运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,
运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力, 取
取 .
.
(1)求框架开始运动时 速度
速度 的大小;
的大小;
(2)从 开始运动到框架开始运动的过程中,
开始运动到框架开始运动的过程中, 上产生的热量
上产生的热量 ,求该过程
,求该过程 位移
位移 的大小。
的大小。
一平台的局部如图甲所示,水平面为光滑,竖直面为粗糙,右角上固定一定滑轮,在水平面上放着一质量mA=2.0kg,厚度可忽略不计的薄板A,薄板A长度L="1.5" m,在板A上叠放着质量 =1.0kg,大小可忽略的物块B,物块B与板A之间的动摩擦因数为
=1.0kg,大小可忽略的物块B,物块B与板A之间的动摩擦因数为 =0.6,一轻绳绕过定滑轮,轻绳左端系在物块B上,右端系住物块C,物块C刚好可与竖直面接触。起始时令各物体都处于静止状态,绳被拉直,物块B位于板A的左端点,然后放手,设板A的右端距滑轮足够远,台面足够高,最大静摩擦力等于滑动摩擦力,忽略滑轮质量及其与轴之间的摩擦,g取10m/s2,求
=0.6,一轻绳绕过定滑轮,轻绳左端系在物块B上,右端系住物块C,物块C刚好可与竖直面接触。起始时令各物体都处于静止状态,绳被拉直,物块B位于板A的左端点,然后放手,设板A的右端距滑轮足够远,台面足够高,最大静摩擦力等于滑动摩擦力,忽略滑轮质量及其与轴之间的摩擦,g取10m/s2,求
(1)若物块C质量mc=1.0kg,推理判断板A和物块B在放手后是否保持相对静止;
(2)若物块C质量mc′=3.0kg,从放手开始计时,经过去t=2.0s,物块C下降的高度;
(3)若物块C质量mc=1.0kg,固定住物块B,物块C静止,现剪断轻绳,同时也对物块C施加力F,方向水平向左,大小随时间变化如图乙所示,断绳时刻开始计时,经过t′=2.0s,物块C恰好停止运动,求物块C与竖直面之间的动摩擦因数和此过程中的最大速度。
如图甲、乙所示,传送带上有质量均为m的三个木块1、2、3,中间均用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为 ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运动,三个木块处于平衡状态。求:
,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运动,三个木块处于平衡状态。求:
(1)在图甲状态下,1、3两木块之间的距离是多大?
(2)在图乙状态下,传送带与水平方向夹角为θ,传送带逆时针方向匀速转动,三个木块处于平衡状态,此时细线的拉力是多大?木块1、3之间的距离又是多大?
如图所示,质量 的木块A套在水平杆上,并用轻绳将木块A与质量
的木块A套在水平杆上,并用轻绳将木块A与质量 的小球相连.今用跟水平方向成α=30°角的力
的小球相连.今用跟水平方向成α=30°角的力 ,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s2.求:
,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s2.求:
(1)运动过程中轻绳与水平方向夹角θ;
(2)木块与水平杆间的动摩擦因数μ.
特种兵过山谷的一种方法可化简为如右图所示的模型:将一根长为2d、不可伸长的细绳的两端固定在相距为d的A、B两等高处,悬绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP竖直,则此时甲对滑轮的水平拉力为____________;若甲将滑轮由静止释放,则乙在滑动中速度的最大值为____________。(不计滑轮与绳的质量,不计滑轮的大小及摩擦)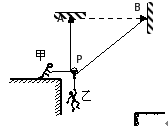
如图甲所示,水平面上的两光滑金属导轨平行固定放置,间距d=0.5 m,电阻不计,左端通过导线与阻值R=2 Ω的电阻连接,右端通过导线与阻值RL=4 Ω的小灯泡L连接。在CDFE矩形区域内有竖直向上的匀强磁场,CE长l=2 m,有一阻值r=2 Ω的金属棒PQ放置在靠近磁场边界CD处(恰好不在磁场中)。CDFE区域内磁场的磁感应强度B随时间变化如图乙所示。在t=0至t=4 s 内,金属棒PQ保持静止,在t=4 s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动。已知从t=0开始到金属棒运动到磁场边界EF处的整个过程中,小灯泡的亮度没有发生变化。求:
(1)通过小灯泡的电流;
(2)金属棒PQ在磁场区域中运动的速度大小。
如图所示,在一矩形区域内有磁感应强度方向垂直纸面向外的匀强磁场,磁感应强度大小为B,磁场宽度为d.不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t,粒子飞出磁场时偏离原方向60°角.利用以上数据能求出的物理量是( )
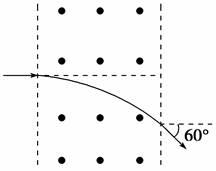
| A.带电粒子在磁场中运动的半径 |
| B.带电粒子的初速度 |
| C.带电粒子在磁场中运动的周期 |
| D.带电粒子的质量 |
如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态. 已知金属棒长L=0.1m,质量m=0.05kg,棒中通有I=10A的向右的电流,取g =10m/s2.
(1)若磁场的磁感应强度B=0.2T,求此时金属棒受到的安培力F的大小;
(2)若细线拉力恰好为零,求磁场的磁感应强度B的大小.
真空中有两个点电荷,相距30cm,它们的电荷量分别是+2.0×10-9C和-4.0×10-9C,问:(1)这两个电荷的相互作用力是引力还是斥力?
(2)这两个电荷的相互作用力多大?