高中物理试题

一带正电荷的质点，在电场力作用下沿曲线abc从a运动到c，已知质点的速率是减小的。关于b点电场强度E的方向，下列图示中符合题意的是（虚线是曲线在b点的切线）（      ）

如图所示，小物体P放在水平圆盘上随圆盘一起转动，下列关于小物体所受摩擦力f的叙述正确的是                （      ）

A．f的方向总是指向圆心

B．圆盘匀速转动时f=0

C．在物体与轴O的距离一定的条件下， f跟圆盘转动的角速度成正比

D．在转速一定的条件下，f跟物体到轴O的距离成正比

在等边三角形的三个顶点a、b、c处，各有一条长直导线垂直穿过纸面，导线中通有大小相等的恒定电流，方向如图。过c点的导线所受安培力的方向         （   ）

A．与ab边平行，竖直向上

B．与ab边平行，竖直向下

C．与ab边垂直，指向左边

D．与ab边垂直，指向右边

如图所示是一个网球沿竖直方向运动时的频闪照片，由照片可知：（   ）

A．网球正在上升	B．网球正在下降
C．网球的加速度向上	D．网球的加速度向下

如图所示，在光滑的水平面上，质量为4m、长为L的木板右端紧靠竖直墙壁，与墙壁不粘连。质量为m的小滑块（可视为质点）以水平速度v₀滑上木板左端，滑到木板右端时速度恰好为零。现小滑块以水平速度v滑上木板左端，滑到木板右端时与竖直墙壁发生弹性碰撞，以原速率弹回，刚好能够滑到木板左端而不从木板上落下，求的值。

某种光学元件由两种不同透明物质Ⅰ和透明物质Ⅱ制成，其横截面如图所示，O为AB中点，=30^o，半圆形透明物质Ⅰ的折射率为n₁=，透明物质Ⅱ的折射率为n₂。一束光线在纸面内沿O点方向射入元件，光线与AB面垂线间的夹角为θ，通过观察发现此时从AC面恰好无光线射出，在BC面有光线垂直射出。求：

①该透明物质Ⅱ的折射率n₂；
②光线在透明物质Ⅱ中的传播速度大小；
③光线与AB面垂线间的夹角θ的正弦值。

如图所示，一个绝热的气缸竖直放置，内有一个绝热且光滑的活塞，中间有一个固定的导热性良好的隔板，隔板将气缸分成两部分，分别密封着两部分理想气体 A 和 B。活塞的质量为m，横截面积为S，与隔板相距h。现通过电热丝缓慢加热气体，当A气体吸收热量Q时，活塞上升了h，此时气体的温度为T₁。已知大气压强为P₀，重力加速度为g。

①加热过程中，若A气体内能增加了ΔE₁，求B气体内能增加量ΔE₂
②现停止对气体加热，同时在活塞上缓慢添加砂粒，当活塞恰好回到原来的位置时A气体的温度为T₂。求此时添加砂粒的总质量Δm。

如图所示的实验装置可以探究加速度与物体质量、物体受力的关系（摩擦力已平衡）。小车上固定一个盒子，盒子内盛有沙子。沙桶的总质量（包括桶以及桶内沙子质量）记为m，小车的总质量（包括车、盒子及盒内沙子质量）记为M。

（1）验证在质量不变的情况下，加速度与合外力成正比：从盒子中取出一些沙子，装入沙桶中，称量并记录沙桶的总重力mg，将该力视为合外力F，对应的加速度a则从打下的纸带中计算得出。多次改变合外力F的大小，每次都会得到一个相应的加速度。以合外力F为横轴，以加速度a为纵轴，画出a－F图象，图象是一条过原点的直线。
在本次实验中，如果沙桶的总重力mg与Mg相比非常接近时，获得的实验数据是否会和理论预期产生较大差异？
答：       ．（填“会”或“不会”）理由是                       。
（2）验证在合外力不变的情况下，加速度与质量成反比：保持桶内沙子质量m不变，在盒子内添加或去掉一些沙子，验证加速度与质量的关系。用图象法处理数据时，以加速度a为纵横，应该以       为横轴。

随着地球资源的日益匮乏和环境的日益恶劣，人类设想在地球远地轨道上建立一个未来的圆环形太空城。远远看去，好像一个巨大的车轮，圆环形的直径为D，“轮胎”是一个空心的大圆环，其内部直径为d（D>d），是太空城的生活区。同时，太空城还绕着自己的中心轴慢慢旋转，利用旋转时产生的离心效应而制造出人造重力，生活在其中的人类就有脚踏实地的感觉。已知地球半径R，表面重力加速度为g，地球自转周期为T，空间站轨道半径r。下列说法中正确的是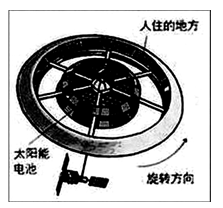

A．太空城中的“地面”在图示的下表面

B．当太空城稳定地转动时，若在“生活区”上空某处静止释放一个物体，让太空城里的你来观察，你会观察到物体沿径向垂直太空城外边缘加速下落

C．若忽略太空城的自转，则太空城的绕地球转动的周期为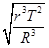

D．若太空城的转速刚能提供和地球表面的实际重力加速度效果相同的人 造“重力”，那么太空城自转的角速度为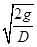

根据玻尔假设，若规定无穷远处的能量为0，则量子数为n的氢原子的能量，E₁为基态的能量，经计算为－13.6 eV，现规定氢原子处于基态时的能量为0，则

A．量子数n＝2时能级的能量为0

B．量子数n＝3时能级的能量为

C．若要使氢原子从基态跃迁到第4能级，则需要吸收的光子能量为

D．若采用能量为的高速电子轰击而跃迁到激发态，这些氢原子从激发态向低能级跃迁的过程中可释放出10种不同频率的光子

高台滑雪以其惊险刺激而闻名，运动员在空中的飞跃姿势具有很强的观赏性．某滑雪轨道的完整结构可以简化成如图所示的示意图．其中AB段是助滑雪道，倾角α＝30°，BC段是水平起跳台，CD段是着陆雪道，AB段与BC段圆滑相连，DE段是一小段圆弧（其长度可忽略），在D、E两点分别与CD、EF相切，EF是减速雪道，倾角θ＝37°．轨道各部分与滑雪板间的动摩擦因数均为μ＝0．25，图中轨道最高点A处的起滑台距起跳台BC的竖直高度h＝10 m．A点与C点的水平距离L₁＝20 m，C点与D点的距离为32．625 m．运动员连同滑雪板的总质量m＝60 kg．滑雪运动员从A点由静止开始起滑，通过起跳台从C点水平飞出，在落到着陆雪道上时，运动员靠改变姿势进行缓冲使自己只保留沿着陆雪道的分速度而不弹起．除缓冲外运动员均可视为质点，设运动员在全过程中不使用雪杖助滑，忽略空气阻力的影响，取重力加速度g＝10 m/s²，sin 37°＝0．6，cos 37°＝0．8．求：

（1）运动员在着陆雪道CD上的着陆位置与C点的距离．
（2）运动员滑过D点时的速度大小．

如图所示，抗震救灾运输机在某场地卸放物资时，通过倾角为30⁰的固定光滑斜轨道面进行。有一件质量为m=2.0kg的小包装盒，由静止开始从斜轨道的顶端A滑至底端B，然后又在水平面上滑行一段距离后停下。若A点距离水平面的高度h=5.0m，重力加速度g取10m/s²,求：

（1）包装盒由A滑到B所经历的时间;
（2）若地面的动摩擦因数为0.5，包装盒在水平地面上还能滑行多远？（不计斜面和地面接触处的能量损耗）

中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T=s。问该中子星的最小密度应是多少才能维持该星的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。（引力常数G=6．6710m/kg．s）

甲、乙两个同学在直跑道上进行4×100 m接力（如图所示），他们在奔跑时有相同的最大速度，乙从静止开始全力奔跑需跑出25 m才能达到最大速度，这一过程可看作匀加速直线运动．现在甲持棒以最大速度向乙奔来，乙在接力区伺机全力奔出．若要求乙接棒时奔跑的速度达到最大速度的80%，则：

（1）乙在接力区须奔出多少距离？
（2）乙应在距离甲多远时起跑？

水平地面上有两个固定的、高度相同的粗糙斜面甲和乙，底边长分别为L₁、L₂，且L₁＜L₂，如图所示。两个完全相同的小滑块A、B（可视为质点）与两个斜面间的动摩擦因数相同，将小滑块A、B分别从甲、乙两个斜面的顶端同时由静止开始释放，取地面所在的水平面为参考平面，则

A．从顶端到底端的运动过程中，由于克服摩擦而产生的热量一定相同
B．滑块A到达底端时的动能一定比滑块Ｂ到达底端时的动能大
C．两个滑块加速下滑的过程中，到达同一高度时，机械能可能相同
D．两个滑块从顶端运动到底端的过程中，重力对滑块A做功的平均功率比滑块B的大