已知等腰三角形的周长是10,底边长 是腰长 的函数,则下列图象中,能正确反映 与 之间函数关系的图象是
A.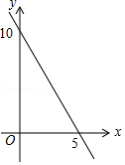 B.
B.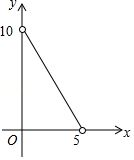
C. D.
D.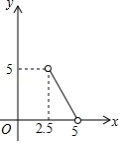
已知一个三角形的两边长分别为8和2,则这个三角形的第三边长可能是
A.4B.6C.8D.10
一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是
A.12B.9C.13D.12或9
(1)阅读理解:
如图①,在 中,若 , ,求 边上的中线 的取值范围.
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ,把 、 , 集中在 中,利用三角形三边的关系即可判断.
中线 的取值范围是 ;
(2)问题解决:
如图②,在 中, 是 边上的中点, 于点 , 交 于点 , 交 于点 ,连接 ,求证: ;
(3)问题拓展:
如图③,在四边形 中, , , ,以 为顶点作一个 角,角的两边分别交 , 于 、 两点,连接 ,探索线段 , , 之间的数量关系,并加以证明.

已知实数 , 满足 ,则以 , 的值为两边长的等腰三角形的周长是
A.20或16B.20
C.16D.以上答案均不对
如图,在 中, ,将 绕顶点 逆时针旋转得到△ , 是 的中点, 是 的中点,连接 .若 , ,则线段 的最大值是
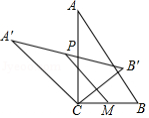
A.4B.3C.2D.1
从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是
A. B. C. D.1
有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是
A. B. C. D.