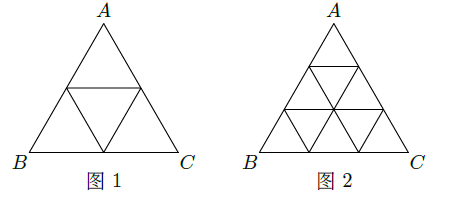
将正 分割成 个全等的小正三角形(图1,图2分别给出了 的情形),在每个三角形的顶点各放置一个数,使位于 的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为 ,则有 , ,…, .
推荐套卷
将正 分割成 个全等的小正三角形(图1,图2分别给出了 的情形),在每个三角形的顶点各放置一个数,使位于 的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为 ,则有 , ,…, .
