推荐套卷
粤ICP备20024846号
 粤公网安备 44130202000953号
粤公网安备 44130202000953号
 粤公网安备 44130202000953号
粤公网安备 44130202000953号
Copyright ©2020-2024 优题课 youtike.com 版权所有
Powered by:Youtike Platform 6.6.3
声明:本网站部分内容由互联网用户自发贡献自行上传,本网站不拥有所有权,也不承担相关法律责任。
如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@youtike.com 或 联系QQ:267757 进行举报,一经查实,本站将立刻删除涉嫌侵权内容。
如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@youtike.com 或 联系QQ:267757 进行举报,一经查实,本站将立刻删除涉嫌侵权内容。
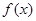 为定义在R上的奇函数,当
为定义在R上的奇函数,当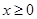 时,
时,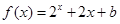 (b为常数),则
(b为常数),则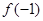 等于( )
等于( )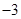

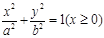 与半椭圆
与半椭圆 合成的曲线称作“果圆”(其中
合成的曲线称作“果圆”(其中
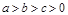 ).如图,设点
).如图,设点 是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为2的等边三角,则a,c的值分别为( )
是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为2的等边三角,则a,c的值分别为( )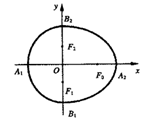
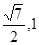

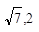
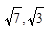
 和双曲线
和双曲线 的离心率为
的离心率为 ,且
,且 成等比数列,下列结论正确的是( )
成等比数列,下列结论正确的是( )



 的焦点且与其对称轴成60º的直线与椭圆交于A,B两点,则|AB|=( ).
的焦点且与其对称轴成60º的直线与椭圆交于A,B两点,则|AB|=( ).



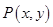 满足
满足 ,过点
,过点 的直线与圆
的直线与圆 相交于
相交于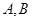 两点,则
两点,则 的最小值为( )
的最小值为( )

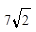


 的一条渐近线平分圆C:(x-1)2+(y-3)2=1的周长,此双曲线的离心率等于( )
的一条渐近线平分圆C:(x-1)2+(y-3)2=1的周长,此双曲线的离心率等于( )

