已知正方体
，点
，
，
分别是线段
，
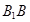和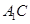
上的动点，观察直线
与
，与
．给出下列结论：
①对于任意给定的点，存在点，使得
；
②对于任意给定的点，存在点，使得
；
③对于任意给定的点，存在点，使得
；
④对于任意给定的点，存在点，使得．
其中正确结论的个数是（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
推荐套卷
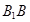已知正方体，点，，分别是线段，和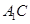上的动点，观察直线与，与．给出下列结论：
①对于任意给定的点，存在点，使得；
②对于任意给定的点，存在点，使得；
③对于任意给定的点，存在点，使得；
④对于任意给定的点，存在点，使得．
其中正确结论的个数是（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
粤公网安备 44130202000953号