有一个公用电话亭，在观察使用这个电话的人的流量时，设在某一时刻，有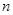
个人正在使用电话或等待使用的概率为
，且与时刻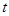
无关，统计得到
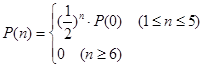，那么在某一时刻这个公用电话亭里一个人也没有的概率
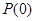的值是（ ）
| A．0 | B．1 | C． |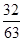
D． |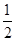
在
上恒满足
，则
的取值范围是
的前
项和为
，
，则实数
的值是
∈（
,
），sin
,则tan（
）等于
的定义域为
的图像大致是（）
推荐套卷
有一个公用电话亭，在观察使用这个电话的人的流量时，设在某一时刻，有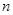个人正在使用电话或等待使用的概率为，且与时刻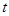无关，统计得到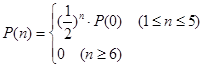，那么在某一时刻这个公用电话亭里一个人也没有的概率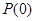的值是（ ）
| A．0 | B．1 | C． |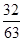
D． |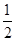
粤公网安备 44130202000953号