欧拉公式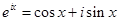
（
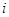为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，
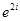表示的复数在复平面中位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
满足约束条件
则目标函数
的最大值为
：
和圆
：
的公切线条数为
，则
，则
则
，则
的前
项和
，则
的圆心为
，且经过原点
，则圆
推荐套卷
欧拉公式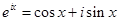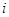（为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知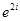，表示的复数在复平面中位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
粤公网安备 44130202000953号