定义在 上的函数
上的函数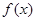 满足:对
满足:对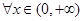 ,都有
,都有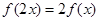 ;当
;当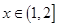 时,
时,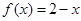 ,给出如下结论:其中所有正确结论的序号是: .
,给出如下结论:其中所有正确结论的序号是: .
①对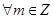 ,有
,有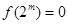 ;
;
②函数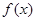 的值域为
的值域为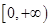 ;
;
③存在 ,使得
,使得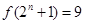 ;
;
④函数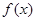 在区间
在区间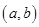 单调递减的充分条件是“存在
单调递减的充分条件是“存在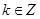 ,使得
,使得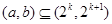 ”.
”.
相关知识点
推荐套卷
定义在 上的函数
上的函数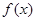 满足:对
满足:对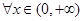 ,都有
,都有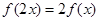 ;当
;当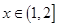 时,
时,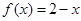 ,给出如下结论:其中所有正确结论的序号是: .
,给出如下结论:其中所有正确结论的序号是: .
①对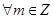 ,有
,有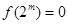 ;
;
②函数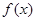 的值域为
的值域为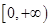 ;
;
③存在 ,使得
,使得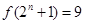 ;
;
④函数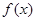 在区间
在区间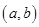 单调递减的充分条件是“存在
单调递减的充分条件是“存在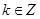 ,使得
,使得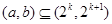 ”.
”.