某军工企业生产一种精密电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：R（x）=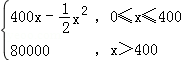
其中x是仪器的月产量．
（1）将利润表示为月产量的函数；
（2）当月产量为何值时，公司所获利润最大？最大利润是多少元？（总收益=总成本+利润．）
在原点相切，若函数的极小值为
；
与
，
，
所围成的平面图形的面积。
.求函数
在
上的最大值和最小值。
在
上是增函数，求a的取值范围.
为偶函数，且在区间
上是单调减函数（Ⅰ）求函数
；（Ⅱ）讨论
的奇偶性.推荐套卷
某军工企业生产一种精密电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：R（x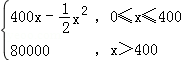）=其中x是仪器的月产量．
（1）将利润表示为月产量的函数；
（2）当月产量为何值时，公司所获利润最大？最大利润是多少元？（总收益=总成本+利润．）
粤公网安备 44130202000953号