已知抛物线 ,过焦点且垂直
,过焦点且垂直 轴的弦长为6,抛物线上的两个动点
轴的弦长为6,抛物线上的两个动点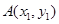 和
和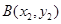 ,其中
,其中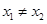 且
且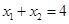 ,线段
,线段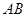 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点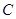 .
.
(1)求抛物线方程;
(2)试证线段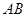 的垂直平分线经过定点,并求此定点;
的垂直平分线经过定点,并求此定点;
(3)求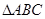 面积的最大值.
面积的最大值.
相关知识点
推荐套卷
已知抛物线 ,过焦点且垂直
,过焦点且垂直 轴的弦长为6,抛物线上的两个动点
轴的弦长为6,抛物线上的两个动点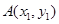 和
和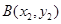 ,其中
,其中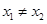 且
且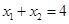 ,线段
,线段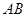 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点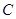 .
.
(1)求抛物线方程;
(2)试证线段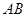 的垂直平分线经过定点,并求此定点;
的垂直平分线经过定点,并求此定点;
(3)求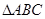 面积的最大值.
面积的最大值.