关于圆周率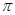
，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计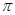的值：先请120名同学，每人随机写下一个都小于1 的正实数对
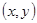；再统计两数能与1构成钝角三角形三边的数对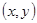的个数
；最后再根据统计数来估计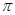的值．假如统计结果是
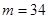，那么可以估计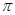为 ．（用分数表示）
价格降低
，问现在价格为8100元的计算机经过15年后，价格应降为＿＿＿＿＿＿＿
，则
="" 
=""
恒过定点推荐套卷
关于圆周率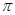，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计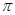的值：先请120名同学，每人随机写下一个都小于1 的正实数对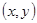；再统计两数能与1构成钝角三角形三边的数对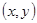的个数；最后再根据统计数来估计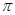的值．假如统计结果是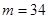，那么可以估计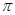为 ．（用分数表示）
粤公网安备 44130202000953号