定义在（0，＋∞）上的函数f （x），对于任意的m，n∈（0，＋∞），都有f （mn）＝f （m）＋f （n）成立，当x >1时，f （x）< 0．
（1）求证：1是函数 f （x）的零点；
（2）求证：f （x）是（0，＋∞）上的减函数；
（3）当f （2）＝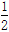 
时，解不等式f （ax＋4）>1．
上一点
，它到左准线的距离为
，求点
上任何一点到两条渐近线的距离之积为定值．
的一底边
在平面
内，另一底边
在平面
到平面
，若
，求
到平面
的左、右两个焦点分别为
，点
在双曲线上，且
，求
的面积．
为抛物线
的顶点，
为这条抛物线互相垂直的两条动弦．
必过一定点．相关知识点
推荐套卷
定义在（0，＋∞）上的函数f （x），对于任意的m，n∈（0，＋∞），都有f （mn）＝f （m）＋f （n）成立，当x >1时，f （x）< 0．
（1）求证：1是函数 f （x）的零点；
（2）求证：f （x）是（0，＋∞）上的减函数；
（3）当f （2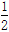）＝ 时，解不等式f （ax＋4）>1．
粤公网安备 44130202000953号