如图所示，在斜三棱柱ABC－A1B1C1的底面△ABC中，∠A＝90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）
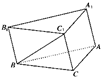
| A．直线AC上 | B．直线AB上 |
| C．直线BC上 | D．△ABC内部 |
则
（）
在
上有零点，则
的取值范围为（）
，若
是实数，且
，则
的最小值为（）
的图像，只需将函数
的图像（）
个单位
个单位
，且
与
垂直，则
等于（）
相关知识点
推荐套卷
如图所示，在斜三棱柱ABC－A1B1C1的底面△ABC中，∠A＝90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）
| A．直线AC上 | B．直线AB上 |
| C．直线BC上 | D．△ABC内部 |
粤公网安备 44130202000953号