（本小题满分10分）设命题p：函数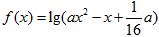
的定义域为R，
命题q：双曲线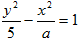
的离心率
,
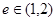（1）如果p是真命题，求实数
的取值范围；
（2）如果命题“p或q”为真命题，且命题“p且q”为假命题，求实数的取值范围．
，求
的值．
的一部分图像如图所示，如果
．
的解析式；
，求
以原点为圆心，且与圆
外切．
与圆
．
的值
与
垂直，求实数
的值．
，求下列各式的值：
；
．相关知识点
推荐套卷
（本小题满分10分）设命题p：函数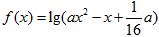的定义域为R，
命题q：双曲线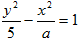的离心率,
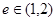（1）如果p是真命题，求实数的取值范围；
（2）如果命题“p或q”为真命题，且命题“p且q”为假命题，求实数的取值范围．
粤公网安备 44130202000953号