某果园现有100棵果树，平均每一棵树结600个果子．根据经验估计，每多种一颗树，平均每棵树就会少结5个果子．设果园增种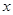
棵果树，果园果子总个数为
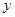个，则果园里增种 棵果树，果子总个数最多．
的最大值为.
，若
,则
．
恒成立，则
的取值范围是.
，
和
是方程
的两个根，那么
．相关知识点
推荐套卷
某果园现有100棵果树，平均每一棵树结600个果子．根据经验估计，每多种一颗树，平均每棵树就会少结5个果子．设果园增种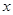棵果树，果园果子总个数为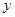个，则果园里增种 棵果树，果子总个数最多．
粤公网安备 44130202000953号