如图所示,半径R=0.8m的1/4光滑圆弧轨道固定在竖直平面内,过最低点的半径OC处于竖直位置,在其右方有一可绕竖直轴MN(与圆弧轨道共面)转动的,内部空心的圆筒,圆筒半径 ,筒的顶端与圆弧轨道最低点C点等高,在筒的下部有一小孔,距筒顶h=0.8m,开始时小孔在图示位置(与圆弧轨道共面)。现让一质量m=0.1kg的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变。此后,小物块沿圆弧轨道滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔。已知A点、B点到圆心O的距离均为R,与水平方向的夹角θ均为30°,不计空气阻力,g取10m/s2。试问:
,筒的顶端与圆弧轨道最低点C点等高,在筒的下部有一小孔,距筒顶h=0.8m,开始时小孔在图示位置(与圆弧轨道共面)。现让一质量m=0.1kg的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变。此后,小物块沿圆弧轨道滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔。已知A点、B点到圆心O的距离均为R,与水平方向的夹角θ均为30°,不计空气阻力,g取10m/s2。试问:
(1)小物块到达C点时的对轨道的压力大小是多少?
(2)圆筒匀速转动时的角速度是多少?
(3)假使小物块进入小孔后,圆筒立即停止转动且恰好沿切线方向进入圆筒内部的光滑半圆轨道,且半圆轨道与圆筒在D点相切。求:圆轨道的半径,并判断小物块能否到达半圆轨道的最高点E点,请说明理由。
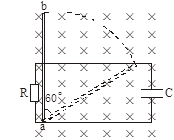
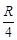 ,杆长为l,A端与环相接触,一电阻为
,杆长为l,A端与环相接触,一电阻为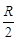 的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。
的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围。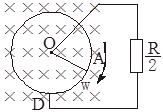
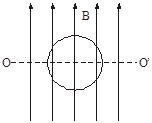

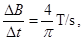 ,求L2的功率。
,求L2的功率。 粤公网安备 44130202000953号
粤公网安备 44130202000953号