如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=mC=3mB,A、B用细绳连接,中间有一压缩的轻弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v0运动,C静止。某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起最终三滑块之间距离不变。求B与C碰撞前B的速度及最终的速度。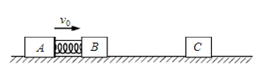
如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=mC=3mB,A、B用细绳连接,中间有一压缩的轻弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v0运动,C静止。某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起最终三滑块之间距离不变。求B与C碰撞前B的速度及最终的速度。