（本小题满分14分）某农场计划种植甲、乙两个品种的蔬菜，总面积不超过
亩，总成本不超过
万元．甲、乙两种蔬菜的成本分别是每亩
元和每亩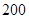
元．假设种植这两个品种的蔬菜，能为该农场带来的收益分别为每亩
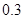万元和每亩
万元．问该农场如何分配甲、乙两种蔬菜的种植面积，可使农场的总收益最大，最大收益是多少万元？
；
（2）若
为
上的动点，
与平面
所成最大角的正切值为
，求锐二面角
的余弦值；
，求点
到平面
的距离。
；（Ⅱ）求三棱锥
的侧面积。
与平面
且平行于平面
的一个截面，并说明理由；推荐套卷
（本小题满分14分）某农场计划种植甲、乙两个品种的蔬菜，总面积不超过亩，总成本不超过万元．甲、乙两种蔬菜的成本分别是每亩元和每亩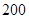元．假设种植这两个品种的蔬菜，能为该农场带来的收益分别为每亩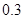万元和每亩万元．问该农场如何分配甲、乙两种蔬菜的种植面积，可使农场的总收益最大，最大收益是多少万元？
粤公网安备 44130202000953号