（本小题满分12分）下表是随机抽取的某市五个地段五种不同户型新电梯房面积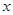
（单位：十平方米）和相应的房价
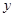（单位：万元）统计表：
|
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
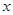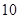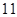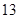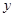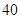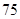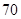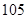（Ⅰ）在给定的坐标系中画出散点图；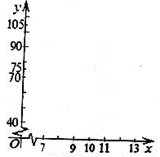
（Ⅱ）求用最小二乘法得到的回归直线方程（参考公式和数据：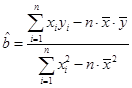
，
，
）；
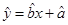（Ⅲ）请估计该市一面积为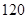
的新电梯房的房价．
相关试题
为等差数列
的前
项和，已知
．
；
．
．
时，求
在区间
上的最值；
时，有
恒成立，求
的取值范围．
为自然对数的底数
．
的最小值；
对任意的
恒成立，求实数
的值．
．
的单调区间；
时，
恒成立，求实数
的取值范围．
方程
在
上有解，命题
只有一个实数
满足不等式
，若命题“
”是假命题，求实数
的取值范围．推荐套卷
（本小题满分12分）下表是随机抽取的某市五个地段五种不同户型新电梯房面积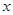（单位：十平方米）和相应的房价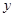（单位：万元）统计表：
|
|
|
|
|
|
|
|
|
|
|
|
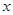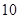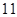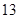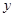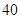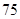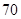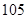（Ⅰ）在给定的坐标系中画出散点图；
（Ⅱ）求用最小二乘法得到的回归直线方程（参考公式和数据：，，）；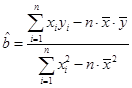
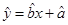（Ⅲ）请估计该市一面积为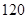的新电梯房的房价．
粤公网安备 44130202000953号