如图所示，在平面直角坐标系xOy中，一次函数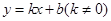
的图象与反比例函数
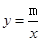的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（-6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=
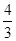，求△AOB的面积．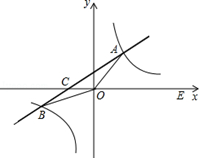
，求
的值
(2) a2－b2＋2b－1
推荐套卷
如图所示，在平面直角坐标系xOy中，一次函数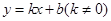的图象与反比例函数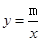的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（-6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=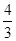，求△AOB的面积．
粤公网安备 44130202000953号