【2015高考重庆，文20】如图，三棱锥P-ABC中，平面PAC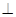
平面ABC，
ABC=
，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC．
（Ⅰ）证明：AB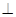平面PFE．
（Ⅱ）若四棱锥P-DFBC的体积为7，求线段BC的长．
推荐套卷
【2015高考重庆，文20】如图，三棱锥P-ABC中，平面PAC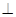平面ABC，ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC．
（Ⅰ）证明：AB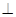平面PFE．
（Ⅱ）若四棱锥P-DFBC的体积为7，求线段BC的长．
粤公网安备 44130202000953号