【2015高考上海,文22】本题共3个小题,第1小题4分,第2小题6分,第3小题6分.
已知椭圆 ,过原点的两条直线
,过原点的两条直线 和
和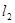 分别于椭圆交于
分别于椭圆交于 、
、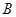 和
和 、
、 ,设
,设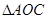 的面积为
的面积为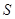 .
.
(1)设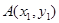 ,
,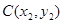 ,用
,用 、
、 的坐标表示点
的坐标表示点 到直线
到直线 的距离,并证明
的距离,并证明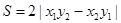 ;
;
(2)设 ,
,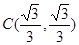 ,
,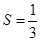 ,求
,求 的值;
的值;
(3)设 与
与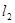 的斜率之积为
的斜率之积为 ,求
,求 的值,使得无论
的值,使得无论 与
与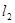 如何变动,面积
如何变动,面积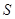 保持不变.
保持不变.
推荐套卷
【2015高考上海,文22】本题共3个小题,第1小题4分,第2小题6分,第3小题6分.
已知椭圆 ,过原点的两条直线
,过原点的两条直线 和
和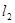 分别于椭圆交于
分别于椭圆交于 、
、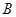 和
和 、
、 ,设
,设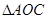 的面积为
的面积为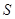 .
.
(1)设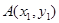 ,
,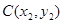 ,用
,用 、
、 的坐标表示点
的坐标表示点 到直线
到直线 的距离,并证明
的距离,并证明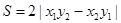 ;
;
(2)设 ,
,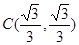 ,
,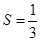 ,求
,求 的值;
的值;
(3)设 与
与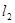 的斜率之积为
的斜率之积为 ,求
,求 的值,使得无论
的值,使得无论 与
与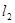 如何变动,面积
如何变动,面积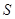 保持不变.
保持不变.