【2015高考浙江,文19】如图,已知抛物线 ,圆
,圆 ,过点
,过点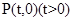 作不过原点O的直线PA,PB分别与抛物线
作不过原点O的直线PA,PB分别与抛物线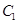 和圆
和圆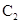 相切,A,B为切点.
相切,A,B为切点.
(1)求点A,B的坐标;
(2)求 的面积.
的面积.
注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公
共点为切点.
推荐套卷
【2015高考浙江,文19】如图,已知抛物线 ,圆
,圆 ,过点
,过点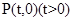 作不过原点O的直线PA,PB分别与抛物线
作不过原点O的直线PA,PB分别与抛物线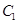 和圆
和圆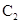 相切,A,B为切点.
相切,A,B为切点.
(1)求点A,B的坐标;
(2)求 的面积.
的面积.
注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公
共点为切点.