(本小题满分13分)设椭圆C: 的离心率
的离心率 ,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
(1)求椭圆C的方程;
(2)若椭圆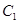 的方程为
的方程为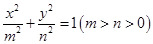 ,椭圆
,椭圆 的方程为
的方程为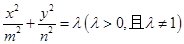 ,则称椭圆
,则称椭圆 是椭圆
是椭圆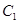 的
的 倍相似椭圆.已知椭圆
倍相似椭圆.已知椭圆 是椭圆C的3倍相似椭圆.若椭圆C的任意一条切线
是椭圆C的3倍相似椭圆.若椭圆C的任意一条切线 交椭圆
交椭圆 于M,N两点,O为坐标原点,试研究当切线
于M,N两点,O为坐标原点,试研究当切线 变化时
变化时 面积的变化情况,并给予证明.
面积的变化情况,并给予证明.
推荐套卷
(本小题满分13分)设椭圆C: 的离心率
的离心率 ,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
(1)求椭圆C的方程;
(2)若椭圆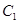 的方程为
的方程为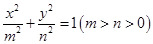 ,椭圆
,椭圆 的方程为
的方程为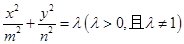 ,则称椭圆
,则称椭圆 是椭圆
是椭圆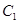 的
的 倍相似椭圆.已知椭圆
倍相似椭圆.已知椭圆 是椭圆C的3倍相似椭圆.若椭圆C的任意一条切线
是椭圆C的3倍相似椭圆.若椭圆C的任意一条切线 交椭圆
交椭圆 于M,N两点,O为坐标原点,试研究当切线
于M,N两点,O为坐标原点,试研究当切线 变化时
变化时 面积的变化情况,并给予证明.
面积的变化情况,并给予证明.