选修4-4： 坐标系与参数方程
在极坐标系中， 已知圆C的圆心C（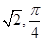
）， 半径r =
．
（Ⅰ）求圆C的极坐标方程；
（Ⅱ）若 α ∈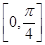
， 直线
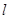的参数方程为
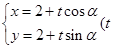为参数）， 直线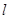交圆C于A、 B两点， 求弦长|AB|的取值范围．
．
的单调增区间；
时，求
的值域．
的最小值为1，且
.
上单调，求
的取值范围．
；
，求
的值。
={
}，
={
}，
的取值范围
，写出用
表示
的关系等式，并证明这个关系等式．相关知识点
推荐套卷
选修4-4： 坐标系与参数方程
在极坐标系中， 已知圆C的圆心C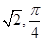（）， 半径r =．
（Ⅰ）求圆C的极坐标方程；
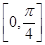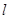（Ⅱ）若 α ∈， 直线的参数方程为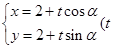为参数）， 直线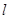交圆C于A、 B两点， 求弦长|AB|的取值范围．
粤公网安备 44130202000953号