(本小题满分15分)如图甲, 是边长为6的等边三角形,
是边长为6的等边三角形, ,
, 分别为
分别为 、
、 靠近
靠近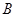 、
、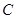 的三等分点,点
的三等分点,点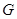 为
为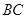 边的中点.线段
边的中点.线段 交线段
交线段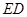 于
于 点,将
点,将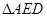 沿
沿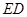 翻折,使平面
翻折,使平面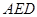 ⊥平面
⊥平面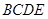 ,连接
,连接 、
、 、
、 形成如图乙所示的几何体.
形成如图乙所示的几何体.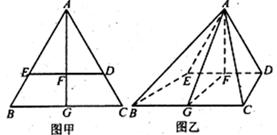
(Ⅰ)求证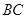 ⊥平面
⊥平面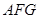 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
相关知识点
推荐套卷
(本小题满分15分)如图甲, 是边长为6的等边三角形,
是边长为6的等边三角形, ,
, 分别为
分别为 、
、 靠近
靠近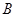 、
、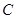 的三等分点,点
的三等分点,点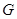 为
为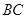 边的中点.线段
边的中点.线段 交线段
交线段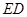 于
于 点,将
点,将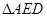 沿
沿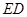 翻折,使平面
翻折,使平面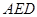 ⊥平面
⊥平面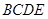 ,连接
,连接 、
、 、
、 形成如图乙所示的几何体.
形成如图乙所示的几何体.
(Ⅰ)求证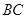 ⊥平面
⊥平面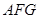 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.