【原创】设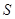 ,
,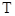 是
是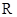 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从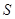 到
到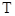 的函数
的函数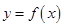 满足:
满足:
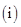
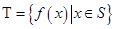 ;
;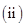 对任意
对任意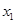 ,
,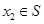 ,当
,当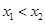 时,恒有
时,恒有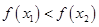 ,那么称这两个集
,那么称这两个集
合“保序同构”.以下集合对是“保序同构”的是( )
A.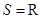 , ,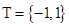 |
B.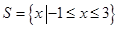 , ,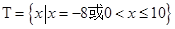 |
C.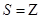 , ,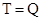 |
D.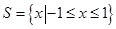 , ,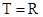 |
推荐套卷
【原创】设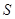 ,
,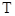 是
是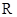 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从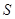 到
到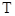 的函数
的函数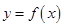 满足:
满足:
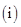
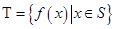 ;
;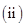 对任意
对任意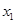 ,
,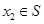 ,当
,当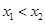 时,恒有
时,恒有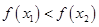 ,那么称这两个集
,那么称这两个集
合“保序同构”.以下集合对是“保序同构”的是( )
A.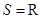 , ,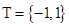 |
B.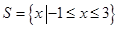 , ,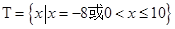 |
C.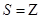 , ,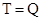 |
D.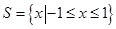 , ,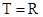 |