定义在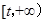 上的函数
上的函数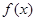 ,
, 单调递增,
单调递增,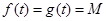 ,若对任意
,若对任意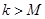 ,存在
,存在 ,
,
使得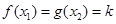 成立,则称
成立,则称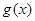 是
是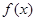 在
在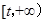 上的“追逐函数”.已知
上的“追逐函数”.已知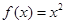 ,下列四个函数:
,下列四个函数:
①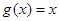 ;②
;②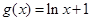 ;③
;③ ;④
;④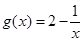 .其中是
.其中是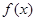 在
在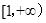 上的“追逐函数”
上的“追逐函数”
的有
A.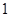 个 个 |
B.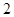 个 个 |
C.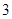 个 个 |
D. 个 个 |
相关知识点
推荐套卷
定义在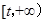 上的函数
上的函数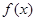 ,
, 单调递增,
单调递增,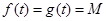 ,若对任意
,若对任意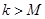 ,存在
,存在 ,
,
使得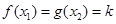 成立,则称
成立,则称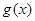 是
是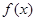 在
在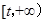 上的“追逐函数”.已知
上的“追逐函数”.已知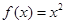 ,下列四个函数:
,下列四个函数:
①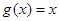 ;②
;②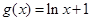 ;③
;③ ;④
;④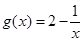 .其中是
.其中是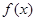 在
在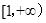 上的“追逐函数”
上的“追逐函数”
的有
A.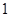 个 个 |
B.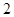 个 个 |
C.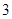 个 个 |
D. 个 个 |