(本小题满分12分)已知函数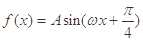 (其中
(其中 ,
, ,
, )的最大值为2,最小正周期为
)的最大值为2,最小正周期为 .
.
(Ⅰ)求函数 的解析式及函数的增区间;
的解析式及函数的增区间;
(Ⅱ)若函数 图象上的两点
图象上的两点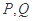 的横坐标依次为
的横坐标依次为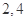 ,
,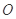 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.
相关知识点
推荐套卷
(本小题满分12分)已知函数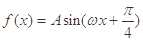 (其中
(其中 ,
, ,
, )的最大值为2,最小正周期为
)的最大值为2,最小正周期为 .
.
(Ⅰ)求函数 的解析式及函数的增区间;
的解析式及函数的增区间;
(Ⅱ)若函数 图象上的两点
图象上的两点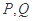 的横坐标依次为
的横坐标依次为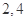 ,
,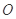 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.