（本小题满分12分）某用人单位招聘员工依次为自荐材料审查、笔试、面试共三轮考核．规定：只能通过前一轮考核后才能进入下一轮的考核，否则将被淘汰；三轮考核都通过才算通过．小王三轮考核通过的概率分别为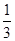
，
，
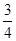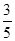，且各轮考核通过与否相互独立．
（1）求小王通过该招聘考核的概率；
（2）若小王通过第一轮考核，家长奖励人民币1200元；若小王通过第二轮考核，家长再奖励人民币1000元；若小王通过第三轮考核，家长再奖励人民币1400元．记小王得到奖励的金额为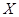
，求
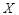的分布列和数学期望．
，且
，求：
及
；
的最小值为
，求实数
的值．
，
，且
，
，求角
的值．
是半径为
，圆心角为
的扇形，
是扇形弧上的动点，
是扇形的内接矩形．记
，求当角
取何值时，矩形
．
上，与
轴相切，且被直线
截得的弦长为
的圆的方程．推荐套卷
（本小题满分12分）某用人单位招聘员工依次为自荐材料审查、笔试、面试共三轮考核．规定：只能通过前一轮考核后才能进入下一轮的考核，否则将被淘汰；三轮考核都通过才算通过．小王三轮考核通过的概率分别为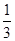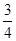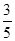，，，且各轮考核通过与否相互独立．
（1）求小王通过该招聘考核的概率；
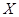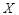（2）若小王通过第一轮考核，家长奖励人民币1200元；若小王通过第二轮考核，家长再奖励人民币1000元；若小王通过第三轮考核，家长再奖励人民币1400元．记小王得到奖励的金额为，求的分布列和数学期望．
粤公网安备 44130202000953号