我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理“幂势既同,则积不容异.”
这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.设由曲线 和直线
和直线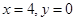 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为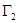 ;根据祖暅原理等知识,通过考察
;根据祖暅原理等知识,通过考察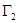 可以得到
可以得到 的体积为 .
的体积为 .
相关知识点
推荐套卷
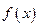 对于任意实数
对于任意实数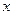 满足条件
满足条件 ,若
,若 则
则 _______________.
_______________.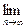 (
(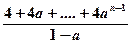 ) =9,则实数
) =9,则实数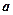 =.
=.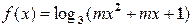 .
.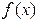 的定义域为R, 则实数m的取值范围是.
的定义域为R, 则实数m的取值范围是. 实数m的取值范围是.
实数m的取值范围是. 的反函数是_______ ___.
的反函数是_______ ___.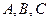 为
为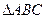 的三个内角,则
的三个内角,则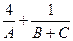 的最小值为.
的最小值为. 粤公网安备 44130202000953号
粤公网安备 44130202000953号