（本小题满分16分）
在平面直角坐标系xOy中，椭圆C：
（a＞b＞0）的上顶点到焦点的距离为2，离心率为
．
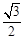（1）求a，b的值．
（2）设P是椭圆C长轴上的一个动点，过点P作斜率为k的直线l交椭圆C于A、B两点．
（ⅰ）若k＝1，求△OAB面积的最大值；
（ⅱ）若PA2＋PB2的值与点P的位置无关，求k的值．
相关试题
的图象过点（0，-3），且
的解集
.
的解析式；
的最值.
,为使满足条件的
的值(1)存在;(2)有且只有一个;(3)有两个不同的值;(4)有三个不同的值,分别求
的取值范围.
．
的最小正周期和最大值；
、
是方程
的两根，且
、
终边互相垂直. 求
的值.
是R上的奇函数，且最小正周期为π.
的值； 
取最小值时的x的集合.推荐套卷
（本小题满分16分）
在平面直角坐标系xOy中，椭圆C：（a＞b＞0）的上顶点到焦点的距离为2，离心率为．
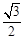（1）求a，b的值．
（2）设P是椭圆C长轴上的一个动点，过点P作斜率为k的直线l交椭圆C于A、B两点．
（ⅰ）若k＝1，求△OAB面积的最大值；
（ⅱ）若PA2＋PB2的值与点P的位置无关，求k的值．
粤公网安备 44130202000953号