某次网球比赛分四个阶段，只有上一阶段的胜者，才能参加继续下一阶段的比赛，否则就被淘汰，选手每闯过一个阶段，个人积10分，否则积0分．甲、乙两个网球选手参加了此次比赛．已知甲每个阶段取胜的概率为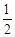
，乙每个阶段取胜的概率为
．
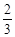（1）求甲、乙两人最后积分之和为20分的概率；
（2）设甲的最后积分为X，求X的分布列和数学期望.
是等比数列；
是等差数列，
，求数列
的前n项和Sn.
中，
是其前
项和，
，求：
及
.推荐套卷
某次网球比赛分四个阶段，只有上一阶段的胜者，才能参加继续下一阶段的比赛，否则就被淘汰，选手每闯过一个阶段，个人积10分，否则积0分．甲、乙两个网球选手参加了此次比赛．已知甲每个阶段取胜的概率为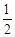，乙每个阶段取胜的概率为．
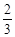（1）求甲、乙两人最后积分之和为20分的概率；
（2）设甲的最后积分为X，求X的分布列和数学期望.
粤公网安备 44130202000953号