给出下列四个命题:
①命题 的否定是
的否定是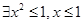 ;
;
②函数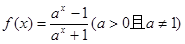 在
在 上单调递减;
上单调递减;
③设 是
是 上的任意函数, 则
上的任意函数, 则 |
|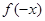 | 是奇函数,
| 是奇函数, +
+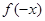 是偶函数;
是偶函数;
④定义在 上的函数
上的函数 对于任意
对于任意 的都有
的都有 ,则
,则 为周期函数;
为周期函数;
⑤已知幂函数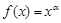 的图象经过点
的图象经过点 ,则
,则 的值等于
的值等于
其中真命题的序号是 (把所有真命题的序号都填上)。
相关知识点
推荐套卷
给出下列四个命题:
①命题 的否定是
的否定是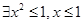 ;
;
②函数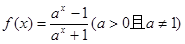 在
在 上单调递减;
上单调递减;
③设 是
是 上的任意函数, 则
上的任意函数, 则 |
|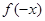 | 是奇函数,
| 是奇函数, +
+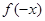 是偶函数;
是偶函数;
④定义在 上的函数
上的函数 对于任意
对于任意 的都有
的都有 ,则
,则 为周期函数;
为周期函数;
⑤已知幂函数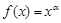 的图象经过点
的图象经过点 ,则
,则 的值等于
的值等于
其中真命题的序号是 (把所有真命题的序号都填上)。