在平面直角坐标系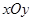 中,已知任意角
中,已知任意角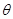 以x轴的正半轴为始边,若终边经过点P
以x轴的正半轴为始边,若终边经过点P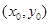 且
且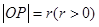 ,定义:
,定义: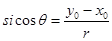 ,称“
,称“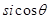 ”为“正余弦函数”对于正余弦函数y=sicosx,有同学得到以下性质:
”为“正余弦函数”对于正余弦函数y=sicosx,有同学得到以下性质:
①该函数的值域为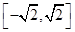 ;
;
②该函数图象关于原点对称;
③该函数图象关于直线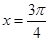 对称;
对称;
④该函数的单调递增区间为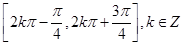 ,
,
则这些性质中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
相关知识点
推荐套卷
在平面直角坐标系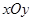 中,已知任意角
中,已知任意角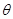 以x轴的正半轴为始边,若终边经过点P
以x轴的正半轴为始边,若终边经过点P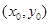 且
且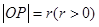 ,定义:
,定义: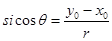 ,称“
,称“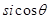 ”为“正余弦函数”对于正余弦函数y=sicosx,有同学得到以下性质:
”为“正余弦函数”对于正余弦函数y=sicosx,有同学得到以下性质:
①该函数的值域为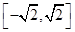 ;
;
②该函数图象关于原点对称;
③该函数图象关于直线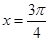 对称;
对称;
④该函数的单调递增区间为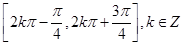 ,
,
则这些性质中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |