(本小题满分12分)某公司研发甲、乙两种新产品,根据市场调查预测,甲产品的利润y(单位:万元)与投资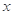 (单位:万元)满足:
(单位:万元)满足: (
(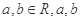 为常数),且曲线
为常数),且曲线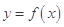 与直线
与直线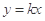 在(1,3)点相切;乙产品的利润与投资的算术平方根成正比,且其图像经过点(4,4).
在(1,3)点相切;乙产品的利润与投资的算术平方根成正比,且其图像经过点(4,4).
(1)分别求甲、乙两种产品的利润与投资资金间的函数关系式;
(2)已知该公司已筹集到40万元资金,并将全部投入甲、乙两种产品的研发,每种产品投资均不少于10万元.问怎样分配这40万元投资,才能使该公司获得最大利润?其最大利润约为多少万元?
(参考数据: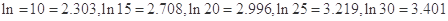 )
)
推荐套卷
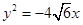 的焦点为F1.
的焦点为F1.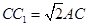 .
.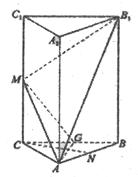
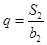 .(Ⅰ)求an与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an与bn;(Ⅱ)设数列{cn}满足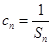 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.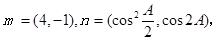

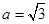 ,试判断b·c取得最大值时△ABC形状.
,试判断b·c取得最大值时△ABC形状. 粤公网安备 44130202000953号
粤公网安备 44130202000953号