以下四个命题中:
①已知随机变量 ,且P
,且P ,P
,P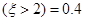 ,则P(
,则P(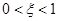 )的值为
)的值为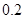 ;
;
②命题“存在 ,使得
,使得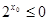 ”的否定是对任意
”的否定是对任意 ,使得
,使得
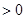 ;
;
③“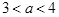 ”是“函数
”是“函数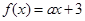 在
在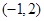 上存在零点”的必要不充分条件;
上存在零点”的必要不充分条件;
④已知平面向量 ,
,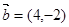 ,
, 与
与 垂直,则
垂直,则 .
.
其中真命题的个数为
推荐套卷
以下四个命题中:
①已知随机变量 ,且P
,且P ,P
,P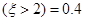 ,则P(
,则P(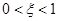 )的值为
)的值为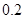 ;
;
②命题“存在 ,使得
,使得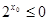 ”的否定是对任意
”的否定是对任意 ,使得
,使得
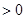 ;
;
③“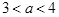 ”是“函数
”是“函数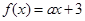 在
在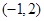 上存在零点”的必要不充分条件;
上存在零点”的必要不充分条件;
④已知平面向量 ,
,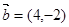 ,
, 与
与 垂直,则
垂直,则 .
.
其中真命题的个数为