设有平面α,β,γ两两互相垂直,且α,β,γ三个平面有一个公共点A,现有一个半径为1的小球与α,β,γ这三个平面均相切,则小球上任一点到点A的最近距离为( )
A.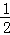 |
B.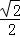 |
C.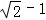 |
D.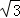 ﹣1 ﹣1 |
推荐套卷
设有平面α,β,γ两两互相垂直,且α,β,γ三个平面有一个公共点A,现有一个半径为1的小球与α,β,γ这三个平面均相切,则小球上任一点到点A的最近距离为( )
A.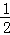 |
B.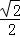 |
C.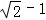 |
D.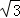 ﹣1 ﹣1 |