若以曲线y=f(x)上任一点M(x1,y1)为切点作切线l1,曲线上总存在异于M的点N(x2,y2),以点N为切点作切线l2,且l1∥l2,则称曲线y=f(x)具有“可平行性”.现有下列命题:
①函数y=(x-2)2+lnx的图象具有“可平行性”;
②定义在(-∞,0)∪(0,+∞)的奇函数y=f(x)的图象都具有“可平行性”;
③三次函数f(x)=x3-x2+ax+b具有“可平行性”,且对应的两切点M(x1,y1),N(x2,y2)的坐标满足x1+x2= ;
;
④要使得分段函数f(x)= 的图象具有“可平行性”,当且仅当实数m=1.
的图象具有“可平行性”,当且仅当实数m=1.
其中的真命题是_______________.(写出所有真命题的序号)
推荐套卷
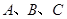 三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到
三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到 班,那么不同的分配方案数为________.(请用数字作答)
班,那么不同的分配方案数为________.(请用数字作答)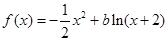 在(-1,+∞)上是减函数,则
在(-1,+∞)上是减函数,则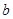 的取值范围是______.
的取值范围是______. ,复数
,复数 是纯虚数,则
是纯虚数,则 ________.
________. ( ).
( ). 粤公网安备 44130202000953号
粤公网安备 44130202000953号