如图，取一个底面半径和高都为R的圆柱，从圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥，把所得的几何体与一个半径为R的半球放在同一水平面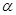
上.用一平行于平面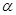的平面去截这两个几何体，截面分别为圆面和圆环面（图中阴影部分）.设截面面积分别为
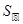和
，那么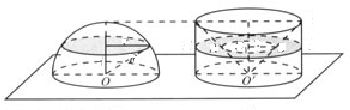
A． |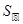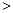
B．= |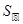
C． |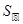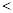
D．不确定 |
相关试题
的
图象按向量
平移后所得的图象关于点
中心对称，则向量
( )
．
C．
D．
，
，且
，则点
的坐标为 ( )
中，
为
的中
点，已知
，
，则下列向量一定与
同向的是 ( )
和实数
，下
列命题中真命题是 ( )
，则
或
，则
或
，则
或
，则
，
，
，则
等于 ( )
相关知识点
推荐套卷
如图，取一个底面半径和高都为R的圆柱，从圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥，把所得的几何体与一个半径为R的半球放在同一水平面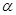上.用一平行于平面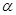的平面去截这两个几何体，截面分别为圆面和圆环面（图中阴影部分）.设截面面积分别为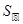和，那么
| A． |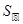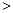
B．= |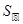
C． |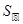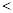
D．不确定 |
粤公网安备 44130202000953号