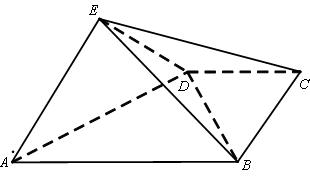
(本小题满分12分)(理科做)如图,四棱锥 中,平面
中,平面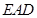
 平面
平面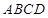 ,
,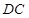 //
//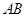 ,
, ,
, ,且
,且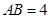 ,
,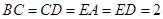 .
.
(1)求证: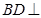 平面
平面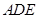 ;
;
(2)求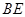 和平面
和平面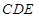 所成角的正弦值;
所成角的正弦值;
(3)在线段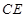 上是否存在一点
上是否存在一点 使得平面
使得平面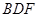
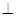 平面
平面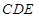 ,请说明理由.
,请说明理由.
(文科做)已知函数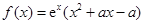 ,其中
,其中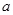 是常数.
是常数.
(1)当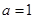 时,求曲线
时,求曲线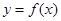 在点
在点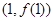 处的切线方程;
处的切线方程;
(2)若存在实数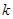 ,使得关于
,使得关于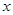 的方程
的方程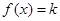 在
在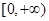 上有两个不相等的实数根,求
上有两个不相等的实数根,求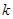 的取值范围.
的取值范围.
推荐套卷
(本小题满分12分)(理科做)如图,四棱锥 中,平面
中,平面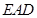
 平面
平面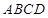 ,
,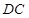 //
//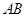 ,
, ,
, ,且
,且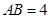 ,
,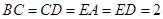 .
.
(1)求证: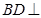 平面
平面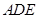 ;
;
(2)求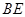 和平面
和平面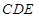 所成角的正弦值;
所成角的正弦值;
(3)在线段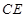 上是否存在一点
上是否存在一点 使得平面
使得平面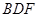
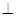 平面
平面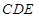 ,请说明理由.
,请说明理由.
(文科做)已知函数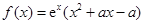 ,其中
,其中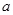 是常数.
是常数.
(1)当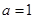 时,求曲线
时,求曲线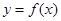 在点
在点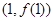 处的切线方程;
处的切线方程;
(2)若存在实数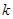 ,使得关于
,使得关于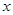 的方程
的方程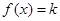 在
在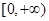 上有两个不相等的实数根,求
上有两个不相等的实数根,求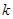 的取值范围.
的取值范围.